��Ŀ����
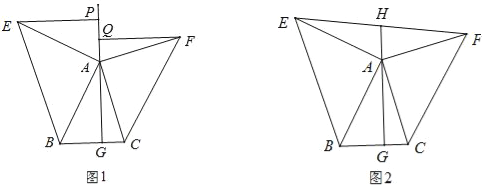
����Ŀ����ͼ1����ABC�У�AG��BC�ڵ�G����AΪֱ�Ƕ��㣬�ֱ���AB��ACΪֱ�DZߣ�����ABC������Rt��ABE�͵���Rt��ACF������E��F������GA�Ĵ��ߣ�����ֱ�ΪP��Q��
��1����֤����AEP�ա�BAG��
��2����̽��EP��FQ֮���������ϵ����֤����Ľ��ۣ�
��3����ͼ2��������EF��GA���ӳ�����H���ɣ�2���еĽ��������ж�EH��FH�Ĵ�С��ϵ�𣿲�˵�����ɣ�
���𰸡���1��֤������������2��EP=FQ��֤������������3��EH=FH�����ɼ�����.
�������������������1�����ݵ���Rt��ABE�����ʣ������EPA=��EAB=��AGB=90������PEA=��BAG������AAS�Ƴ���EPA�ա�AGB��
��2������ȫ�������ε������Ƴ�EP=AG��ͬ���ɵ���FQA�ա�AGC�����ɵó�AG=FQ���������������ɵó��𰸣�
��3�������EPH=��FQH=90��������AAS�Ƴ���EPH�ա�FQH�����ɵó�EH��FH�Ĵ�С��ϵ��
�����������1����ͼ1���ߡ�EAB=90����EP��AG��AG��BC��
���EPA=��EAB=��AGB=90����
���PEA+��EAP=90������EAP+��BAG=90����
���PEA=��BAG��
����EPA����AGB��
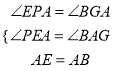 ��
��
���EPA�ա�AGB��AAS����
��2��EP=FQ��
֤�����ɣ�1���ɵã���EPA�ա�AGB��
��EP=AG��
ͬ���ɵã���FQA�ա�AGC��
��AG=FQ��
��EP=FQ��
��3��EH=FH��
���ɣ���ͼ����EP��AG��FQ��AG��
���EPH=��FQH=90����
����EPH����FQH��
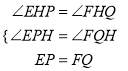 ��
��
���EPH�ա�FQH��AAS����
��EH=FH��

����Ŀ����5�֣���2015����ɽ��ĩ��С��ij���ֻ������еĸ������ͳ�����������ͼ�����������ͼ����Ϣ������и��⣺
��Ŀ | �¹��ܷ� | �������� | ��;���� | ���ŷ� |
���/Ԫ | 5 | 50 |
��1���뽫����������
��2���뽫����ͳ��ͼ����������
��3������ͳ��ͼ�У���ʾ���ŷѵ����ε�Բ�Ľ��Ƕ��ٶȣ�


