题目内容
【题目】如图,在△ABC中,CA=CB,∠ACB=90°,D为AB边上的中点,M,N分别为AC,BC上的点,且DM![]() DN,试说明AB=2(CM+CN)。
DN,试说明AB=2(CM+CN)。

【答案】见解析
【解析】试题分析:(1)根据等腰直角三角形的性质和等腰直角三角形斜边上的中线性质得到∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,再利用等角的余角相等得到∠CDM=∠BDN,然后根据“ASA”可判断△CMD≌△BDN,则CM=BN,又由AC=BC可得AM=CN,即CM+CN=AC=AB,在直角△ABC中AC2+BC2=AB2,即2AC2=AB2,根据等量代换可得:AB=2(CM+CN).
试题解析:
如图,连接CD,
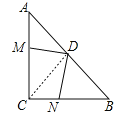
∵△ACB是等腰直角三角形,D为斜边AB的中点,
∴∠A=∠B=∠ACD=∠DCB=45°,AC=BC,CD⊥AB,CD=BD=AD,
∴∠CDB=90°,
∵DM⊥DN,
∴∠MDN=90°,
∴∠MDC=∠BDN=90°-∠CDN,
在△CMD和△BND中,
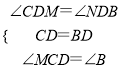 ,
,
∴△CMD≌△BND(ASA),
∴DM=BN,
又∵AC=BC,
∴AM=CN,
∴CM+CN=AC=AB,
在直角△ABC中AC2+BC2=AB2,
∴2AC2=AB2,
∴AB=2(CM+CN).

练习册系列答案
相关题目