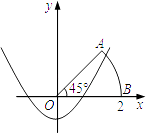题目内容
【题目】如图,已知直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y= ![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( )
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为( ) 
A.(2,4)
B.(1,8)
C.(2,4)或(1,8)
D.(2,4)或(8,1)
【答案】D
【解析】解:∵点B(﹣4,﹣2)在双曲线y= ![]() 上, ∴
上, ∴ ![]() =﹣2,
=﹣2,
∴k=8,
∴双曲线的函数解析式为y= ![]() .
.
过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
∵正比例函数与反比例函数的交点A、B关于原点对称,
∴A(4,2),
∴OE=4,AE=2,
设点C的坐标为(a, ![]() ),则OF=a,CF=
),则OF=a,CF= ![]() ,
,
当a<4时,则S△AOC=S△COF+S梯形ACFE﹣S△AOE ,
= ![]() ×a×
×a× ![]() +
+ ![]() (2+
(2+ ![]() )(4﹣a)﹣
)(4﹣a)﹣ ![]() ×4×2
×4×2
= ![]() ,
,
∵△AOC的面积为6,
∴ ![]() =6,
=6,
整理得a2+6a﹣16=0,
解得a=2或﹣8(舍弃),
∴点C的坐标为(2,4).
当a>4时,则S△AOC=S△COF+S梯形ACFE﹣S△AOE ,
= ![]() ×a×
×a× ![]() +
+ ![]() (2+
(2+ ![]() )(a﹣4)﹣
)(a﹣4)﹣ ![]() ×4×2
×4×2
= ![]() ,
,
∵△AOC的面积为6,
∴ ![]() =6,
=6,
整理得a2﹣6a﹣16=0,
解得a=﹣2(舍去)或8,
∴点C的坐标为(8,1).
故选D.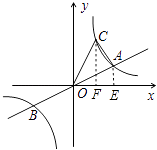

【题目】“十 一”黄金周期间,我市庐山风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数)
日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
(1)、若9月30日的游客人数记为n,请用含n的代数式表示10月2日的游客________万人。
(2)、请判断七天内游客人数最多的是_______日;最少的是______日;它们相差_____万人。
(3)、以9月30日的游客人数为0点,用折线统计图表示这7天的游客人数变化情况: