题目内容
【题目】如图,PA、PB、AB都与⊙O相切,∠P=60°,则∠AOB等于( ) 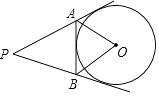
A.50°
B.60°
C.70°
D.70°
【答案】B
【解析】解:设PA、PB、AB与⊙O相切于E、D、C,连接OE、OD、OC,如图, ∴PA、PB、AB都与⊙O相切,
∴OE⊥AB,OD⊥PB,OC⊥PA,
∴∠COD=180°﹣∠P=120°,
在Rt△AOC和Rt△AOE中![]() ,
,
∴Rt△AOC≌Rt△AOE,
同理可得△OBD≌△OBE,
∴∠AOC=∠AOE,∠BOD=∠BOE,
∴∠AOB= ![]() COD=60°.
COD=60°.
故选B.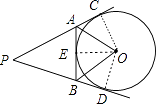
设PA、PB、AB与⊙O相切于E、D、C,连接OE、OD、OC,如图,根据切线的性质得OE⊥AB,OD⊥PB,OC⊥PA,利用四边形的内角和可计算出∠COD=120°,再证△OAC≌△OAE,△OBD≌△OBE得到∠AOC=∠AOE,∠BOD=∠BOE,所以∠AOB= ![]() COD=60°.
COD=60°.

练习册系列答案
相关题目