题目内容
直线y=px（p是不等于0的整数）与直线y=x+10的交点恰好是整点（横坐标和纵坐标都是整数），那么满足条件的直线有
- A.6条
- B.7条
- C.8条
- D.无数条
B
分析：联立直线y=px与直线y=x+10，求出p的取值范围即可求得结果．
解答：联立直线y=px与直线y=x+10，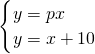
，
得px=x+10，x=
，
∵x为整数，p也为整数．
∴P的取值范围为：-9≤P≤11，且P≠1，P≠0．
而.10=2×5=1×10，
0＜P≤11，有四条直线，
P≠0，-9≤P＜0，只有三条直线，
那么满足条件的直线有7条．
故选B．
点评：本题考查了两条直线相交或平行问题，难度较大，关键不要漏掉某条直线．
分析：联立直线y=px与直线y=x+10，求出p的取值范围即可求得结果．
解答：联立直线y=px与直线y=x+10，
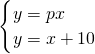，得px=x+10，x=
，∵x为整数，p也为整数．
∴P的取值范围为：-9≤P≤11，且P≠1，P≠0．
而.10=2×5=1×10，
0＜P≤11，有四条直线，
P≠0，-9≤P＜0，只有三条直线，
那么满足条件的直线有7条．
故选B．
点评：本题考查了两条直线相交或平行问题，难度较大，关键不要漏掉某条直线．
练习册系列答案
名校通行证有效作业系列答案
相关题目
直线y=px（p是不等于0的整数）与直线y=x+10的交点恰好是整点（横坐标和纵坐标都是整数），那么满足条件的直线有（ ）
| A、6条 | B、7条 | C、8条 | D、无数条 |
=BO，BC∥x轴．
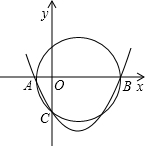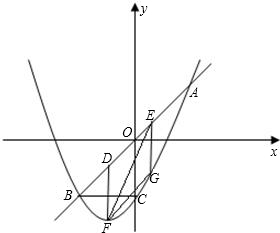
（1998•东城区）如图，在直角坐标系xoy中，A、B是x轴上两点，以AB为直径的圆交y轴于C点，设过A、B、C三点的抛物线解析式为y=x2-px+q，若方程x2-px+q=0两根的倒数和为-2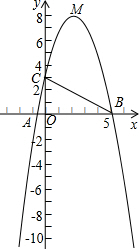
如图，二次函数y=-x2+px+q的图象与x轴交于A、B两点，与y轴交于点C（0，3），顶点M在第一象限，∠ABC=30°．