��Ŀ����
��ͼ����֪y=| 1 |
| 2 |
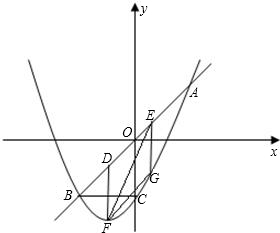 =BO��BC��x�ᣮ
=BO��BC��x�ᣮ��1����p��q��ֵ��
��2����D��E���߶�AB������A��B���������㣨��E�ڵ�D�����Ϸ�����DE=
| 2 |
�����D�ĺ�����Ϊt����EDF�����ΪS����S��t֮��ĺ�����ϵʽ���Ա���t��ȡֵ��Χ��
���ֹ���E��y���ƽ���ߣ�����������G�������ܲ����ʵ�ѡ���D��λ�ã�ʹ�ı���DFGE��ƽ���ı��Σ�����ܣ������ʱ��D�����ꣻ������ܣ���˵�����ɣ�
��������1���������C��0��q��������BC��x�ᣬ�ҵ�B��ֱ��y=x�ϣ�����õ�B�����꣬��OA=BO֪����A��B����ԭ��Գƣ���õ�A�����꣬Ȼ����뺯������ʽ���������p��q��ֵ��˶��κ����Ľ���ʽ��
��2�����ɵ�Dֱ��x=t��y=x�ϣ�����õ�D�����꣬����F��ֱ��x=t�ϣ�����������y=
x2+x-2�ϣ����ɵõ�F�����꣬Ȼ�����E��EH��DF���ӳ�����H����DE=
��֪��EH=1��S=
DF•EH��������ô𰸣�
����֪E��t+1��t+1��������G��ֱ��x=t+1�ϣ�����������y=
x2+x-2�ϣ�����֪��G��������EG�ij������ı���DFGE��ƽ���ı��Σ���EG=DF���������t��ֵ����ɵ����������ĵ�D���ڣ�������Ϊ��-
��-
����
��2�����ɵ�Dֱ��x=t��y=x�ϣ�����õ�D�����꣬����F��ֱ��x=t�ϣ�����������y=
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
����֪E��t+1��t+1��������G��ֱ��x=t+1�ϣ�����������y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
����⣺��1���������C��0��q����
��BC��x�ᣬ�ҵ�B��ֱ��y=x�ϣ�
��y=
x2+px+q����֪����B������Ϊ��q��q����
��OA=BO֪����A��B����ԭ��Գƣ�
���A��������-q��-q����
��
��
��ã�p=1��q=-2��
�������ߵĽ���ʽΪ��y=
x2+x-2��
��2���١ߵ�Dֱ��x=t��y=x�ϣ�
�ɣ�1����֪����D������Ϊ��t��t����
����F��ֱ��x=t�ϣ�����������y=
x2+x-2�ϣ�
���F��������t��
t2+t-2����
����E��EH��DF���ӳ�����H����DE=
��֪��EH=1��
DF=t-��
t2+t-2��=-
t2+2��
��S=
DF•EH=
��-
t2+2����1=-
t2+1��
�ⷽ���飺
��
��ã�
��
���A��2��2����B��-2��-2����
��t��ȡֵ��ΧΪ-2��t��1���ҵ�t=0ʱ��S�����ֵ1��
����֪E��t+1��t+1��������G��ֱ��x=t+1�ϣ�����������y=
x2+x-2�ϣ�
��֪��G������Ϊ��t+1��
��t+1��2+��t+1��-2����
��EG=��t+1��-[
��t+1��2+��t+1��-2]=-
t2-t-
��
���ı���DFGE��ƽ���ı��Σ���EG=DF����-
t2-t-
=-
t2+2��
��ã�t=-
��
�����������ĵ�D���ڣ�������Ϊ��-
��-
����
��BC��x�ᣬ�ҵ�B��ֱ��y=x�ϣ�
��y=
| 1 |
| 2 |
��OA=BO֪����A��B����ԭ��Գƣ�
���A��������-q��-q����
��
|
��ã�p=1��q=-2��
�������ߵĽ���ʽΪ��y=
| 1 |
| 2 |
��2���١ߵ�Dֱ��x=t��y=x�ϣ�
�ɣ�1����֪����D������Ϊ��t��t����
����F��ֱ��x=t�ϣ�����������y=
| 1 |
| 2 |
���F��������t��
| 1 |
| 2 |
����E��EH��DF���ӳ�����H����DE=
| 2 |
DF=t-��
| 1 |
| 2 |
| 1 |
| 2 |
��S=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
�ⷽ���飺
|
��ã�
|
|
���A��2��2����B��-2��-2����
��t��ȡֵ��ΧΪ-2��t��1���ҵ�t=0ʱ��S�����ֵ1��
����֪E��t+1��t+1��������G��ֱ��x=t+1�ϣ�����������y=
| 1 |
| 2 |
��֪��G������Ϊ��t+1��
| 1 |
| 2 |
��EG=��t+1��-[
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
���ı���DFGE��ƽ���ı��Σ���EG=DF����-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
��ã�t=-
| 1 |
| 2 |
�����������ĵ�D���ڣ�������Ϊ��-
| 1 |
| 2 |
| 1 |
| 2 |
���������⿼���˶��κ������ۺ�Ӧ�ã������ۺ��Ժ�ǿ���ѶȽϴ���Ĺؼ��Ƿ���˼�������ν��˼���Ӧ�ã�

��ϰ��ϵ�д�
 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�
�����Ŀ
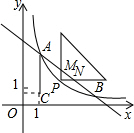
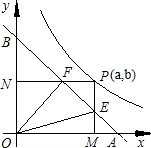 һ�㣬���������ǣ�a��b�����ɵ�P��x�ᡢy�������Ĵ���PM��PN��������M��N��ֱ��AB�ֱ�PM��PN�ڵ�E��F��
һ�㣬���������ǣ�a��b�����ɵ�P��x�ᡢy�������Ĵ���PM��PN��������M��N��ֱ��AB�ֱ�PM��PN�ڵ�E��F��
 ��ͼ����֪��AOB=40�㣬��BOC=80�㣬��OD��OE�ֱ��ǡ�AOB�͡�BOC��ƽ���ߣ�
��ͼ����֪��AOB=40�㣬��BOC=80�㣬��OD��OE�ֱ��ǡ�AOB�͡�BOC��ƽ���ߣ� ��ͼ����ֱ֪��l1��l2�Ľ������꣬������ij������Ľ⣬��ֻ���Ƿ��飨�������Ľ⣮
��ͼ����ֱ֪��l1��l2�Ľ������꣬������ij������Ľ⣬��ֻ���Ƿ��飨�������Ľ⣮