题目内容
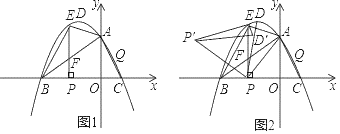
【题目】如图1，在平面直角坐标系中，抛物线y＝﹣
+2与x轴交于B、C两点，与y轴交于点A，抛物线的顶点为D．连接AB，点E是第二象限内的抛物线上的一动点，过点E作EP⊥BC于点P，交线段AB于点F．
（1）连接EA、EB，取线段AC的中点Q，当△EAB面积最大时，在x轴上找一点R使得|RE一RQ|值最大，请求出R点的坐标及|RE﹣RQ|的最大值；
（2）如图2，在（1）的条件下，将△PED绕E点旋转得△ED′P′，当△AP′P是以AP为直角边的直角三角形时，求点P′的坐标．
【答案】（1）
（2）当△AP′P是以AP为直角边的直角三角形时，点P′的坐标为（
，
）或（
，
）或（
，
）
【解析】
（1）先求直线AB解析式，设点E横坐标为e，则能用e表示E、F的坐标进而表示EF，求得△EAB面积是关于e的二次函数，易得e＝﹣
时△EAB面积最大，进而得E的坐标．由三角形两边之差小于第三边可知，当E、Q、R成一直线时，|RE﹣RQ|＝EQ最大；由Q为AC中点求得Q坐标，求直线EQ解析式即能求EQ与x轴的交点R坐标及EQ的长．
（2）设P'坐标为（m、n），由于不确定以点A还是点P为直角顶点，故需分两类情况讨论．每种情况下都易得有关P'、P的三角形与△AOP相似，由对应边成比例列得关于m、n的二元方程；又由旋转得EP'＝EP＝，根据勾股定理又列得关于m、n的二元方程，联立两二元方程组即求出m、n的值．
（1）∵y＝0时，﹣
+2＝0，解得：x1＝﹣3，x2＝1，
∴B（﹣3，0），C（1，0），
∵x＝0时，y＝2，，
∴A（0，2），
设直线AB的解析式为y＝kx+b，
∴
解得：
，
∴直线AB的解析式为：y＝
x+2，
设点E（e，﹣e2﹣
e+2），则点F（e，e+2），
∴EF＝﹣e2﹣e+2﹣（e+2）＝﹣e2﹣2e
∴S△EAB＝
OBEF＝×3（﹣e2﹣2e）＝﹣e2﹣3e＝﹣（e+）2+
，
∵﹣3＜e＜0
∴当e＝﹣时，△EAB的面积最大，
∴﹣e2﹣e+2＝
，
∴此时点E坐标为（-，）
如图1，
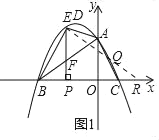
连接并延长EQ，交x轴于点R，则此时|RE﹣RQ|＝EQ值最大
∵Q是AC中点，
∴Q（，1）
设直线EQ解析式为：y＝ax+c，
∴
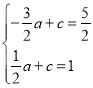，解得：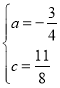
，
∴直线EQ解析式为：y＝
x+
，
当y＝0时， x+＝0，解得：x＝
，
∴R（，0），
此时|RE﹣RQ|的最大值EQ＝
，
（2）设点P'坐标为（m，n）
∵EP⊥x轴，E（-，）
∴P（-，0），EP＝，AP＝
，
i）当∠P'PA＝90°时，如图2，
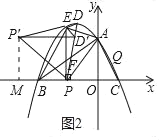
过点P'作P'M⊥x轴于点M，
∴∠P'MP＝∠POA＝90°，∠PP'M+∠P'PM＝∠P'PM+∠APO＝90°，
∴∠PP'M＝∠APO，
∴△PP'M∽△APO，
∴
，即：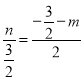
，
整理得：4n+3m＝
①，
∵EP'＝EP
∴（m+）2+（n﹣）2＝（）2②，
联立①②解方程组得：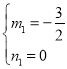
（舍去）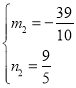
，
∴P'（
，）；
ii）当∠PAP'＝90°时，如图3，过点P'作P'N⊥y轴于点N；
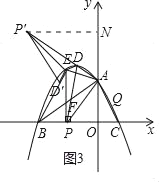
由△P'AN∽△APO得
，即：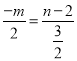
，
整理得：3m+4n＝8①，
∵EP'＝EP，
∴（m+）2+（n﹣）2＝（）2②，
联立①②解方程组得：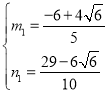
，
，
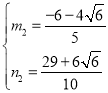∴P'（，）或（，），
综上所述，当△AP′P是以AP为直角边的直角三角形时，点P′的坐标为（ ，）或（，）或（，）
