题目内容
如图，半圆D的直径AB=4，与半圆O内切的动圆O1与AB切于点M，设⊙O1的半径为y，AM=x，则y关于x的函数关系式是 （ ）
A． | B． | C． | D． |
A.
解析试题分析： 连接01M，OO1，可得到直角三角形OO1M，依题意可知⊙O的半径为2，则OO1=2﹣y，OM=2﹣x，O1M=y．在Rt△OO1M中，由勾股定理得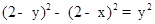
，解得．
故选A．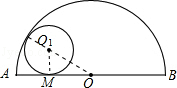
考点：根据实际问题列二次函数关系式．
练习册系列答案
53随堂测系列答案
相关题目
顶点为（-5,0）且平移后能与函数
的图象完全重合的抛物线是（ ）
A． | B． | C． | D． |
如图，抛物线
和直线
. 当y1＞y2时，x的取值范围是（ ）
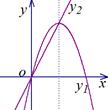
| A．0<x<2 | B．x<0或x＞2 | C．x<0或x＞4 | D．0<x<4 |
将二次函数y=x2的图象向右平移一个单位长度，再向上平移3个单位长度所得的图象解析式为（ ）
| A．y=（x﹣1）2+3 | B．y=（x+1）2+3 |
| C．y=（x﹣1）2﹣3 | D．y=（x+1）2﹣3 |
抛物线y=-x2可由抛物线y=-(x-2)2+3如何平移得到（ ）
| A．先向左平移2个单位，再向下平移3个单位 |
| B．先向右平移2个单位，再向下平移3个单位 |
| C．先向左平移2个单位，再向上平移3个单位 |
| D．先向右平移2个单位，再向上平移3个单位 |
抛物线
与x轴的交点坐标是（ ）
| A．（1，0）（-3，0） | B．（-1，0）（3，0） |
| C．（1，0）（3，0） | D．（-1，0）（-3，0） |
函数
与
在同一坐标系中的大致图象是（ ）
A． | B． | C． | D． |