Question

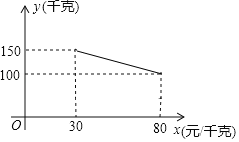
【题目】某超市销售一种商品，成本价为20元/千克，经市场调查，每天销售量y(千克)与销售单价x(元/千克)之间的关系如图所示，规定每千克售价不能低于30元，且不高于80元．

（1）求y与x之间的函数关系式；

（2）设每天的总利润为w元，当销售单价定为多少元时，该超市每天的利润最大？最大利润是多少元？

Answer 1

【答案】（1）y=-x+180；（2）销售单价定为80元时，该超市每天的利润最大，最大利润6000元

【解析】

（1）将点（30，150）、（80，100）代入一次函数表达式，即可求解；
（2）由题意得：w=（x-20）（-x+180）=-（x-100）2+6400，根据二次函数的性质即可求解．

解：（1）将点(30,150)、(80,100)代入一次函数表达式得：

，

解得：，

故函数的表达式为：y=-x+180

（2）由题意得：w=(x-20)(-x+180)=-(x-100)2+6400

∵-1＜0，故当x＜100时，w随x的增大而增大，

∵30≤x≤80，

当x=80时，w取最大值，此时，w=6000．

故销售单价定为80元时，该超市每天的利润最大，最大利润6000元．