题目内容
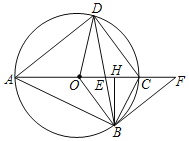
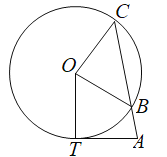
【题目】如图,已知AT切圆O于点T,点B在圆O上,且![]() ,连接AB并延长交圆O于点C,圆O的半径为2,若AT的长恰好为2.
,连接AB并延长交圆O于点C,圆O的半径为2,若AT的长恰好为2.
(1)求证:△BOC是等腰直角三角形;
(2)求AC的长.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)连接BT可证△BOT为等边三角形,得BT=2,∠OTB=∠OBT=60°,进而得出△ABT是顶角为30°的等腰三角形,得出∠TBA=75°,根据平角定义得出∠CBO=45°,从而得到结论;
(2)先根据△OBC是等腰直角三角形求出BC,再证明△ABT∽△ATC,求出AB的长,从而可得出AC的长.
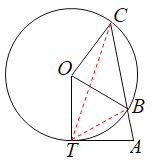
(1)连接BT,
∵∠BOT=60°,OB=OT,
∴△BOT是等边三角形,
∴∠OTB=∠OBT=60°,BT=OB=2,
∵AT是⊙O的切线,
∴∠OTA=90°
∴∠BTA=30°
∵AT=2,
∴AT=BT,
∴∠TBA=![]()
∵∠ABT+∠TBO+∠OBC=180°,
∴∠OBC=180°-∠ABT-∠TBO=180°-75°-60°=45°,
∵OB=OC
∴∠OCB=∠OBC=45°,即∠BOC=90°
∴△BOC是等腰直角三角形;
(2)∵△BOC是等腰直角三角形,OB=OC=2,
∴BC=![]()
连接CT,则∠ACT=![]() ∠BOT,
∠BOT,
由(1)可知,∠ATB=![]() ∠BOT,
∠BOT,
∴∠ATB=∠ACT
又∠A=∠A
∴△ATB∽△ACT
∴![]() ,即
,即![]()
把AT=2,BC=![]() 代入,得
代入,得![]() ,
,
解得,![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴![]() .
.

【题目】对于气温,有的地方用摄氏温度表示,有的地方用华氏温度表示,摄氏温度与华氏温度之间是一次函数关系.如图所示是一个家用温度表的表盘、其左边为摄氏温度的刻度和读数(单位![]() ),右边为华氏温度的刻度和读数(单位
),右边为华氏温度的刻度和读数(单位![]() ).从温度计的刻度上可以看出,摄氏温度
).从温度计的刻度上可以看出,摄氏温度![]() 与华氏温度
与华氏温度![]() 部分对应关系如下表:
部分对应关系如下表:
| ··· |
|
| ··· |
| ··· |
|
| ··· |

(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当摄氏温度为零下![]() 时,求华氏温度为多少?
时,求华氏温度为多少?