Question

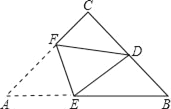
【题目】如图，一块四边形的纸板剪去△DEC，得到四边形ABCE，测得∠BAE =∠BCE=90°，BC=CE，AB=DE．

（1）能否在四边形纸板上只剪一刀，使剪下的三角形与△DEC全等？请说明理由；

（2）求∠D的度数．

Answer 1

【答案】（1）见解析（2）45°.

【解析】

（1）连接AC, 利用全等三角形的判定方法（SAS）进而判断得出答案．

（2）由第（1）△ABC≌△DEC,可得AC=DC, ∠ACB=∠DCE，根据∠BCE=90°, ∠ACB+∠ACE=∠BCE, ∠ACB=∠DCE，∠DCE+∠ACE=∠ACB+∠ACE=∠BCE=90°,

可得∠ACD=90°,继而可得△ADC是等腰直角三角形.

沿AC剪一刀.

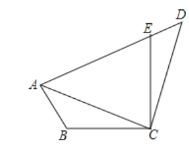
理由：∵∠BAE=∠BCE=90°，

∴∠ABC+∠AEC=180°，

∵∠AEC+∠DEC=180°，

∴∠DEC=∠B，

在△ABC和△DEC中，

AB＝DE，∠B＝∠EDC， BC＝EC，

∴△ABC≌△DEC（SAS）．

（2）∵△ABC≌△DEC,

∴AC=DC, ∠ACB=∠DCE，

∵∠BCE=90°, ∠ACB+∠ACE=∠BCE, ∠ACB=∠DCE，

∴∠DCE+∠ACE=∠ACB+∠ACE=∠BCE=90°,

∴∠ACD=90°,

∵AC=DC,

∴∠D=45°.