题目内容
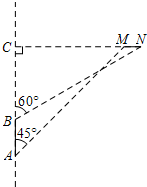
在正方形ABCD中，N是DC的中点，M是AD上异于D的点，且∠NMB=∠MBC，则tan∠ABM=______．
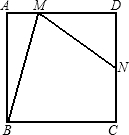
如图：延长MN交BC的延长线于T，设MB的中点为O，连TO，则OT⊥BM，
∵∠ABM+∠MBT=90°，
∠OTB+∠MBT=90°，
∴∠ABM=∠OTB，则△BAM∽△TOB，
∴
=
，即
=
，即MB2=2AM•BT ①
令DN=1，CT=MD=K，则：AM=2-K，BM=
，BT=2+K，
代入①中得：4+（2-K）2=2（2-K）（2+K），
解方程得：K1=0（舍去），K2=
．
∴AM=2-
=
．
tan∠ABM=
=
=
．
故答案是：
．
∵∠ABM+∠MBT=90°，
∠OTB+∠MBT=90°，
∴∠ABM=∠OTB，则△BAM∽△TOB，
∴
| AM |
| OB |
| MB |
| BT |
| AM |
| MB |
| OB |
| BT |
令DN=1，CT=MD=K，则：AM=2-K，BM=
| 4+(2-K)2 |
代入①中得：4+（2-K）2=2（2-K）（2+K），
解方程得：K1=0（舍去），K2=
| 4 |
| 3 |
∴AM=2-
| 4 |
| 3 |
| 2 |
| 3 |
tan∠ABM=
| AM |
| AB |
| ||
| 2 |
| 1 |
| 3 |
故答案是：
| 1 |
| 3 |
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
蓝天教育暑假优化学习系列答案
相关题目
