题目内容
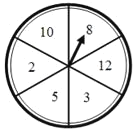
【题目】小亮、小颖的手上都有两根长度分别为5、8的木棒,小亮与小颖都想通过转动转盘游戏来获取第三根木棒,如图,一个均匀的转盘被平均分成6等份,分别标有木棒的长度2,3,5,8,10,12这6个数字.小亮与小颖各转动转盘一次,停止后,指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜,三根木棒能组成等腰三角形则小颖获胜.
(1)小亮获胜的概率是 ;
(2)小颖获胜的概率是 ;
(3)请你用这个转盘设计一个游戏,使得对小亮与小颖均是公平的;
(4)小颖发现,她连续转动转盘10次,都没转到5和8,能不能就说小颖获胜的可能性为0?为什么?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析;(4)不能,理由见解析.
;(3)见解析;(4)不能,理由见解析.
【解析】
(1)设构成三角形的第三根木棒的长度为x,由三角形三边关系可知3<x<13,在所给的6个数字中,有4个数字满足条件,则可求小亮获胜的概率.(2)在所给的6个数字中,有2个数字满足条件,则可求小颖获胜的概率.(3)答案不唯一,只要使得小亮与小颖获胜的概率相同即可.(4)不能,只能说明可能性小,但并不一定为0.
解:
(1)设构成三角形的第三根木棒的长度为x,
则8﹣5<x<5+8,即3<x<13,
∵在2,3,5,8,10,12这6个数字中,能构成三角形的有5、8、10、12这四个,
∴小亮获胜的概率是![]() =
=![]() ,
,
故答案为:![]() .
.
(2)∵在2,3,5,8,10,12这6个数字中,能构成等腰三角形的有5,8这两个,
∴小颖获胜的概率是![]() =
=![]() .
.
(3)小亮转动转盘一次,停止后指针指向的数字即为转出的第三根木棒的长度.若三根木棒能组成三角形则小亮获胜;小颖转动转盘一次,停止后指针指向的数字为偶数,则小颖获胜.
(4)不能,她连续转动转盘10次,都没转到5和8,只是说明可能性小,但并不一定为0.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案