题目内容
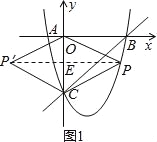
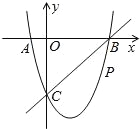
【题目】如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，A点在原点左侧，B点的坐标为（4，0），与y轴交于C（0，﹣4）点，点P是直线BC下方的抛物线上一动点．
（1）求这个二次函数的表达式．
（2）连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C，那么是否存在点P，使四边形POP′C为菱形？若存在，请求出此时点P的坐标；若不存在，请说明理由．
（3）当点P运动到什么位置时，四边形ABPC的面积最大？求出此时P点的坐标和四边形ABPC的最大面积．
【答案】（1）二次函数的表达式为：y=x2﹣3x﹣4；
（2）存在，P点的坐标为（
，﹣2）；
（3）此时P点的坐标为：（2，﹣6），四边形ABPC的面积的最大值为18．
【解析】
试题分析：（1）将B、C的坐标代入抛物线的解析式中即可求得待定系数的值；
（2）由于菱形的对角线互相垂直平分，若四边形POP′C为菱形，那么P点必在OC的垂直平分线上，据此可求出P点的纵坐标，代入抛物线的解析式中即可求出P点的坐标；
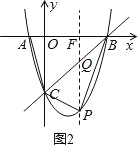
（3）由于△ABC的面积为定值，当四边形ABPC的面积最大时，△BPC的面积最大；过P作y轴的平行线，交直线BC于Q，交x轴于F，易求得直线BC的解析式，可设出P点的横坐标，然后根据抛物线和直线BC的解析式求出Q、P的纵坐标，即可得到PQ的长，以PQ为底，B点横坐标的绝对值为高即可求得△BPC的面积，由此可得到关于四边形ACPB的面积与P点横坐标的函数关系式，根据函数的性质即可求出四边形ABPC的最大面积及对应的P点坐标．
试题解析：（1）将B、C两点的坐标代入得：
，
解得：
；
所以二次函数的表达式为：y=x2﹣3x﹣4；
（2）存在点P，使四边形POP′C为菱形；
设P点坐标为（x，x2﹣3x﹣4），PP′交CO于E
若四边形POP′C是菱形，则有PC=PO；
如图1，连接PP′，则PE⊥CO于E，
∵C（0，﹣4），
∴CO=4，
又∵OE=EC，
∴OE=EC=2
∴y=﹣2；
∴x2﹣3x﹣4=﹣2
解得：x1=
，x2=
（不合题意，舍去），
∴P点的坐标为（，﹣2）；
（3）如图2，过点P作y轴的平行线与BC交于点Q，与OB交于点F，设P（x，x2﹣3x﹣4），设直线BC的解析式为：y=kx+d，
则
，
解得：
，
∴直线BC的解析式为：y=x﹣4，
则Q点的坐标为（x，x﹣4）；
当0=x2﹣3x﹣4，
解得：x1=﹣1，x2=4，
∴AO=1，AB=5，
S四边形ABPC=S△ABC+S△BPQ+S△CPQ
=
ABOC+
QPBF+
QPOF
=
×5×4+
（4﹣x）[x﹣4﹣（x2﹣3x﹣4）]+ 
x[x﹣4﹣（x2﹣3x﹣4）]
=﹣2x2+8x+10
=﹣2（x﹣2）2+18
当x=2时，四边形ABPC的面积最大，
此时P点的坐标为：（2，﹣6），四边形ABPC的面积的最大值为18．
