题目内容
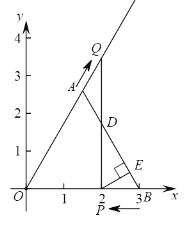
【题目】已知：在平面直角坐标系
中，对于任意的实数
，直线
都经过平面内一个定点
．
（1）求点的坐标．
（2）反比例函数
的图象与直线交于点和另外一点
①求
的值；
②当
时，求
的取值范围
【答案】(1) A(-1,-2)；(2)①b=2， m＞0或m＜-1.
【解析】
(1)解析式化为y=ax+a-2=a(x+1)-2，即可求得；
(2)①根据待定系数法即可求得；②根据反比例函数的性质即可判定点P(m,n)在第一象限或第三象限两种情况，分别讨论即可．
解：（1）∵y=ax+a-2=a(x+1)-2，
∴当x=-1时，y=-2，
∴直线y=ax+a-2都经过平面内一个定点A(-1,-2)；
故答案为：A(-1,-2).
（2）①∵反比例函数
的图像经过点A，
∴b=-1×(-2)=2；
②若点P(m,n)在第一象限，当n＞-2时，m＞0，
若点P(m,n)在第三象限，当n＞-2时，m＜-1，
综上，当n＞-2时，m＞0或m＜-1．
故答案为：b=2，m的取值范围是：m＞0或m＜-1.
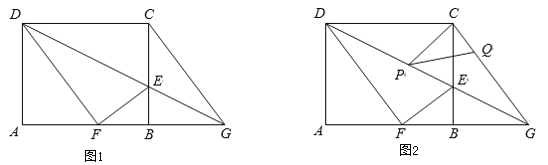
【题目】如图，点
是线段
的中点，
是以为圆心，
长为直径的半圆弧，点
是上一动点，过点作射线
的垂线，垂足为
．已知
，
，设
、两点间的距离为
，、两点间的距离为
，、两点间的距离为
．
小丽根据学习函数的经验，分别对函数
和
随自变量
变化而变化的规律进行了探究．下面是小丽的探究过程，请将它补充完整：
（1）按照下表中自变量的值进行取点、画图、测量，分别得到和与的几组对应值：
| 2 | 3 | 4 | 4.5 | 5 | 5.5 | 6 | 7 | 8 |
| 0 | 2.76 |
| 2.96 | 2.86 | 2.70 | 2.49 | 1.85 | 0 |
| 3.00 | 1.18 | 0 | 0.47 | 0.90 | 1.30 | 1.37 | 2.36 | 3.00 |
经测量，
的值是______；（保留一位小数）
（2）在同一平面直角坐标系
中，描出补全后的表中各组数值所对应的点
和
，并画出函数、的图象；
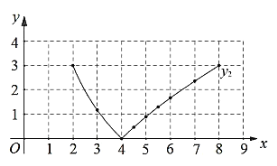
（3）结合函数图象，解决问题：连接
，当
是等腰三角形时，的长度约为______
．（结果保留一位小数）
【题目】改革开放以来，人们的支付方式发生了巨大转变，近年来，移动支付已成为主要的支付方式之一，为了解某校学生上个月
两种移动支付方式的使用情况，从全校
名学生中随机抽取了
人，发现样本中两种支付方式都不使用的有
人，样本中仅使用
种支付方式和仅使用
种支付方式的学生的支付金额
(元)的分布情况如下：
支付金额 支付方式 |
|
|
|
仅使用 |
|
|
|
仅使用 |
|
|
|
下面有四个推断：
①从样本中使用移动支付的学生中随机抽取一名学生，该生使用A支付方式的概率大于他使用B支付方式的概率；
②根据样本数据估计，全校1000名学生中．同时使用A、B两种支付方式的大约有400人；
③样本中仅使用A种支付方式的同学，上个月的支付金额的中位数一定不超过1000元；
④样本中仅使用B种支付方式的同学，上个月的支付金额的平均数一定不低于1000元．其中合理的是（ ）
A.①③B.②④C.①②③D.①②③④
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出：公民科学素质是实施创新驱动发展战略的基础，是国家综合国力的体现．《方案》明确提出，2020年要将我国公民科学素质的数值提升到10%以上．为了解我国公民科学素质水平及发展状况，中国科协等单位已多次组织了全国范围的调查，以下是根据调查结果整理得到的部分信息．注：科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比．
．2015和2018年我国各直辖市公民科学素质发展状况统计图如下：
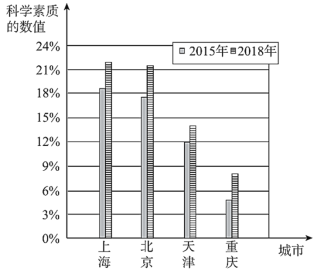
b．2015年和2018年我国公民科学素质发展状况按性别分类统计如下：
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c．2001年以来我国公民科学素质水平发展统计图如下：
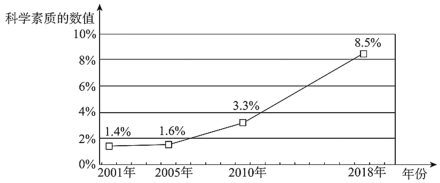
根据以上信息，回答下列问题：
(1)在我国四个直辖市中，从2015年到2018年，公民科学素质水平增幅最大的城市是________，公民科学素质水平增速最快的城市是_________．注：科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值；科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值．
(2)已知在2015年的调查样本中，男女公民的比例约为1：1，则2015年我国公民的科学素质水平为______%(结果保留一位小数)；由计算可知．在2018年的调查样本中．男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”)．
(3)根据截至2018年的调查数据推断，你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由．
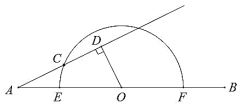
【题目】如图，C是
上的一定点，P是弦AB上的一动点，连接PC，过点A作AQ⊥PC交直线PC于点Q．小石根据学习函数的经验，对线段PC，PA，AQ的长度之间的关系进行了探究．（当点P与点A重合时，令AQ＝0cm）
下面是小石的探究过程，请补充完整：
（1）对于点P在弦AB上的不同位置，画图、测量，得到了线段PC，PA，AQ的几组值，如表：
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | 位置9 | |
PC/cm | 4.07 | 3.10 | 2.14 | 1.68 | 1.26 | 0.89 | 0.76 | 1.26 | 2.14 |
PA/cm | 0.00 | 1.00 | 2.00 | 2.50 | 3.00 | 3.54 | 4.00 | 5.00 | 6.00 |
AQ/cm | 0.00 | 0.25 | 0.71 | 1.13 | 1.82 | 3.03 | 4.00 | 3.03 | 2.14 |
在PC，PA，AQ的长度这三个量中，确定 的长度是自变量， 的长度和 的长度都是这个自变量的函数；
（2）在同一平面直角坐标系xOy中，画出（1）中所确定的函数的图象；
（3）结合函数图象，解决问题：当AQ＝PC时，PA的长度约为 cm．（结果保留一位小数）
