��Ŀ����
����Ŀ����ֱ������ϵ�У�AΪx�Ḻ�����ϵĵ㣬BΪy�Ḻ�����ϵĵ㣮

��1����ͼ�٣���A��Ϊ���㣬ABΪ���ڵ�������������Rt��ABC������֪A����2��0��B��0����4��������C������ꣻ
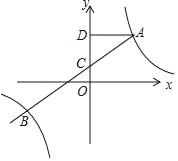
��2����ͼ�ڣ�����A������Ϊ����2![]() ��0������B������Ϊ��0��a������D��������Ϊb����BΪ���㣬BAΪ��������Rt��ABD����B����y�Ḻ���������˶�����������������ʱ����b��a��ֵ��
��0������B������Ϊ��0��a������D��������Ϊb����BΪ���㣬BAΪ��������Rt��ABD����B����y�Ḻ���������˶�����������������ʱ����b��a��ֵ��
��3����ͼ�ۣ�EΪx�Ḻ�����ϵ�һ�㣬��OB��OE��OF��EB�ڵ�F����OBΪ���ڵ����������ȱ���OBM������EM��OF�ڵ�N��̽��EM-ON��EN��������ϵ��
���𰸡���1��C����6����2������2��2![]() ����3��EN��
����3��EN��![]() ��EM��ON�������ɼ�����
��EM��ON�������ɼ�����
��������
��1����CQ��OA�ڵ�Q������֤����AQC�ա�BOA����QC=AO��AQ=BO�����������Ϳ������C�����ꣻ
��2����DP��OB�ڵ�P������֤����AOB�ա�BPD������AO=BP=OB-PO=-a-��-b��=b-aΪ��ֵ��
��3����BH��EB��B�����������Եó���1=30������2=��3=��EMO=15������EOF=��BMG=45����EO=BM������֤����ENO�ա�BGM����GM=ON������EM-ON=EM-GM=EG�������ƽ���߷��߶γɱ��������Ϳ��Եó�EN=EM-ON��һ�룮
��1����ͼ��1����CQ��OA�ڵ�Q��

���AQC��90��
�ߡ�ABC�ǵ���Rt����
��AC��AB����CAB��90����
���ACQ����BAO��
����AQC����BOA��
 ��
��
���AQC�ա�BOA��
��CQ��AO��AQ��BO��
��A����2��0����B��0����4����
��OA��2��OB��4��
��CQ��2��AQ��4��
��OQ��6��
��C����6����2����
��2����ͼ��2����DP��OB�ڵ�P��

���BPD��90����
�ߡ�ABD�ǵ���Rt����
��AB��BD����ABD����ABO+��OBD��90����
���ABO����BDP��
����AOB����BPD��
 ��
��
���AOB�ա�BPD��
��AO��BP��
��BP��OB��PO����a������b����b��a��
��A����2![]() ��0����
��0����
��OA��2![]() ��
��
��b��a��2![]() ��
��
�൱B����y�Ḻ���������˶�ʱAO��BP��b��a��2![]() ��
��
��3����ͼ��3����ME�Ͻ�ȡMG��ON������BG��

�ߡ�OBM�ǵȱ������Σ�
��BO��BM��MO����OBM����OMB����BOM��60����
��EO��MO����EBM��105������1��30����
��OE��OB�� ��OE��OM��BM��
���3����EMO��15����
���BEM��30������BME��45����
��OF��EB��
���EOF��45��
���EOF����BME��
����ENO����BGM��
 ��
��
���ENO�ա�BGM��
��BG��EN��
��ON��MG��
���2����3��
���2��15����
���EBG��90��
��BG��![]() EG��
EG��
��EN��![]() EG��
EG��
��EG��EM��GM��
��EN��![]() ��EM��GM����
��EM��GM����
��EN��![]() ��EM��ON��.
��EM��ON��.