题目内容
【题目】如果一个四位自然数的百位数字大于或等于十位数字，且千位数字等于百位数字与十位数字的和，个位数字等于百位与十位数字的差，则我们称这个四位数为亲密数，例如：自然数4312，其中3＞1，4=3+1，2=3-1，所以4312是亲密数；
（1）最小的亲密数是 ，最大的亲密数是 ；
（2）若把一个亲密数的千位数字与个位数字交换，得到的新数叫做这个亲密数的友谊数，请证明任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除；
（3）若一个亲密数的后三位数字所表示的数与千位数字所表示的数的7倍之差能被13整除，请求出这个亲密数．
【答案】（1）1101，9909；（2）证明见解析；（3）亲密数为5321或9817．
【解析】
（1）设亲密数为
，求最小的亲密数时，先确定a=1，再根据a=b+c，d=b﹣c确定b、c、d的值，从而可得最小的亲密数；求最大的亲密数时，先确定a=9，同理可得最大的亲密数；
（2）分别表示亲密数和友谊数：亲密数：=1000a+100b+10c+d，友谊数：
=1000d+100b+10c+a，相减后可得结论；
（3）根据题意表示
﹣7a=100b+10c+d﹣7a，化为关于b和c的代数式，根据b是1至9的自然数对：94b+2c进行分析，
=7b+
为整数，即3b+2c为13的倍数，分情况讨论3b+2c的值可得结论．
设亲密数为，且b≥c，a=b+c，d=b-c，a、b、c、d都是自然数，
（1）当a为最小时，则a=1，
∴b+c=a=1，
∵b≥c，
∴b=1，c=0，
∴d=b-c=1-0=1，
∴最小的亲密数是1101，
当a最大时，即a=9，
∴b+c=a=9，
∵b≥c，
当
最大时，即b最大为9，
∴c=0，
∴d=b-c=9-0=9，
∴最大的亲密数是9909，
故答案为：1101，9909；
（2）证明：亲密数：
=1000a+100b+10c+d①，
友谊数：
=1000d+100b+10c+a②，
∵a=b+c，d=b-c，
∴a-d=（b+c）-（b-c）=2c＞0，
∴a＞d，a=2c+d，
①-②得：999a-999d=999（a-d）=999（2c+d-d）=1998c，
∵原亲密数的十位数字为c，
∴任意一个亲密数和它的友谊数的差都能被原亲密数的十位数字整除；
（3）=100b+10c+d，
∵a=b+c，d=b-c，
∴-7a=100b+10c+d-7a=100b+10c+b-c-7（b+c）=94b+2c，
由题意得：
为整数，
即3b+2c为13的倍数，
∵0≤b≤9，0≤c≤9，b、c为整数，且1≤b+c≤9，
∴2≤3b+2c≤27，
∴3b+2c=13或26，
①当3b+2c=13时（b≥c），
得
，
∴亲密数为5321；
②若3b+2c=26（b≥c），
则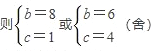
，
∴亲密数为9817，
综上所述，亲密数为5321或9817．
