Question

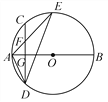
【题目】如图，AB是⊙O的直径，弦CD⊥AB于点G，点F是CD上一点，且满足，连接AF并延长交⊙O于点E，连接AD，DE，若CF＝2，AF＝3，给出下列结论：①△ADF∽△AED；②FG＝2；③tanE＝；④S△DEF＝4.其中正确的是( )

A. ①②③ B. ②③④ C. ①②④ D. ①③④

Answer 1

【答案】C

【解析】试题解析：①∵AB是⊙O的直径，弦CD⊥AB，

∴，DG=CG，

∴∠ADF=∠AED，

∵∠FAD=∠DAE（公共角），

∴△ADF∽△AED；

故①正确；

②∵，CF=2，

∴FD=6，

∴CD=DF+CF=8，

∴CG=DG=4，

∴FG=CG-CF=2；

故②正确；

③∵AF=3，FG=2，

∴AG=，

∴在Rt△AGD中，tan∠ADG=，

∴tan∠E=；

故③错误；

④∵DF=DG+FG=6，AD=，

∴S△ADF=DFAG=×6×=3，

∵△ADF∽△AED，

∴，

∴，

∴S△AED=7，

∴S△DEF=S△AED-S△ADF=4；

故④正确．

故选C．