题目内容
【题目】如图,已知AD是△ABC的中线, DE⊥AB于E, DF⊥AC于F, 且BE=CF, 求证:(1)AD是∠BAC的平分线;(2)AB=AC.

【答案】(1)详见解析;(2)详见解析.
【解析】
可由HL得到RT△BED≌RT△CFD,得出AB=AC,再由三线合一的性质即可得到AD⊥BC.
证明: (1)∵AD是△ABC的中线,∴BD=CD.
在Rt△EBD和Rt△FCD中
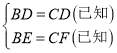
∴Rt△EBD≌Rt△FCD(HL),
∴DE=DF(全等三角形的对应边相等)
在Rt△AED和Rt△AFD中,

∴Rt△AED≌Rt△AFD(HL),
∴∠1=∠2(全等三角形的对应角相等),即AD是∠BAC的平分线.
(2)∵Rt△AED≌Rt△AFD(已证),
∴AE=AF(全等三角形的对应边相等).
又∵BE=CF(已知),
∴AB=AC.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目











