题目内容
已知△ABC的三边长都是整数,且△ABC外接圆的直径为6.25,那么△ABC三边的长是 ________.
5、5、6
分析:设△ABC三边长为a,b,c且a,b,c均为正整数.根据已知条件知三角形的三个边长均小于外接圆直径6.25.然后根据海伦--秦九韶公式 =S=
=S= absinC=
absinC=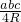 求得64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b),最后由数的整除求得三角形的三个边长.
求得64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b),最后由数的整除求得三角形的三个边长.
解答:设△ABC三边长为a,b,c且a,b,c均为正整数,△ABC外接圆直径2R=6.25.
∵a,b,c≤2R,
∴a,b,c只能取1、2、3、4、5、6;
由 =S=
=S= absinC=
absinC=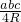 ,得
,得
 •(a+b+c)(b+c-a)(c+a-b)(a+b-c)=
•(a+b+c)(b+c-a)(c+a-b)(a+b-c)=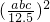
∴64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b)
∴54|(abc)2故a,b,c中至少有两个5;
不妨设a=b=5,则64C2=(10+c)•C•C•(10-c)?C=6,
∴△ABC三边长为5,5,6.
故答案为:5、5、6.
点评:本题主要考查了三角形的三边关系、正弦定理与余弦定理.解答此题时,综合运用了海伦--秦九韶公式与数的整除的知识点.
分析:设△ABC三边长为a,b,c且a,b,c均为正整数.根据已知条件知三角形的三个边长均小于外接圆直径6.25.然后根据海伦--秦九韶公式
 =S=
=S= absinC=
absinC=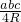 求得64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b),最后由数的整除求得三角形的三个边长.
求得64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b),最后由数的整除求得三角形的三个边长.解答:设△ABC三边长为a,b,c且a,b,c均为正整数,△ABC外接圆直径2R=6.25.
∵a,b,c≤2R,
∴a,b,c只能取1、2、3、4、5、6;
由
 =S=
=S= absinC=
absinC=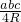 ,得
,得 •(a+b+c)(b+c-a)(c+a-b)(a+b-c)=
•(a+b+c)(b+c-a)(c+a-b)(a+b-c)=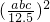
∴64(abc)2=625•(a+b+c)(a+b-c)(b+c-a)(c+a-b)
∴54|(abc)2故a,b,c中至少有两个5;
不妨设a=b=5,则64C2=(10+c)•C•C•(10-c)?C=6,
∴△ABC三边长为5,5,6.
故答案为:5、5、6.
点评:本题主要考查了三角形的三边关系、正弦定理与余弦定理.解答此题时,综合运用了海伦--秦九韶公式与数的整除的知识点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目