Question

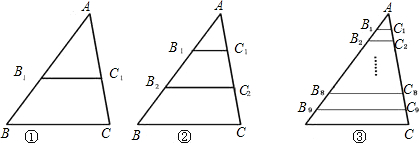
在△ABC中，BC=10，B₁、C₁分别是图①中AB、AC的中点，在图②中，B₁，B₂，C₁，C₂分别是AB，AC的三等分点，在图③中B₁，B₂…B₉；C₁，C₂…C₉分别是AB、AC的10等分点，B₁C₁+B₂C₂+…+B₉C₉的值是（　　）

• A、30
• B、45
• C、55
• D、60

Answer 1

分析：根据相似三角形的性质，和等分点求出边与BC的相似比，找到规律，计算B₁C₁+B₂C₂+…+B₉C₉的和．

解答：解：在图①中，B₁C₁=

1

2

BC，
在图②中，B₁C₁=

1

3

BC，B₂C₂=

2

3

BC，
那么在图③中，B₁C₁=

1

10

BC，B₂C₂=

2

10

BC，…B₉C₉=

9

10

BC，
∴B₁C₁+B₂C₂+…+B₉C₉=BC×

1+2+3+4+5+6+7+8+9

10

=45．
故选B．

点评：本题主要利用相似三角形的性质和等分点求出边与BC的相似比，找出规律是关键．