题目内容
如图:在△ABC中,BC=2AB=4,AD为边BC上的中线,E、F分别为BC、AB上的动点,且CE=BF,EF与AD交于点G.FH⊥AG于H
(1)①如图1,当∠B=90°时,FG
.
②如图2,当∠B=60°时,FG
③如图3,当∠B=α时,FG
AD
AD.
请你先填上空,再从以上三个命题中任选择一个进行证明
(2)如图4,若(1)中的点E、F分别在BC、AB的延长线上,试问(1)中的结论是否仍然成立.若成立,请证明你的结论;若不成立,请说明理由.

(1)①如图1,当∠B=90°时,FG
=
=
EG;GH=| 2 |
| 2 |
②如图2,当∠B=60°时,FG
=
=
EG;GH=1
1
.③如图3,当∠B=α时,FG
=
=
EG;GH=| 1 |
| 2 |
| 1 |
| 2 |
请你先填上空,再从以上三个命题中任选择一个进行证明
(2)如图4,若(1)中的点E、F分别在BC、AB的延长线上,试问(1)中的结论是否仍然成立.若成立,请证明你的结论;若不成立,请说明理由.

分析:(1)①由条件可以求出AB=BD,AF=DE,从而得出∠BAD=∠BDA=45°,求出AD的值,作FQ∥BC,利用平行线的性质得出AF=FQ,根据等腰三角形的性质可以得出AH=HQ,可以证明△FQG≌△EDG,FG=EG,通过计算可以求出GH=
.
②)由条件可以求出AB=BD,AF=DE,从而得出∠BAD=∠BDA=60°,求出AD的值,作FR∥BC,利用平行线的性质得出AF=FR,根据等腰三角形的性质可以得出AH=HR,可以证明△FRG≌△EDG,FG=EG,通过计算可以求出GH=1.
③)由条件可以求出AB=BD,AF=DE,从而得出∠BAD=∠BDA=45°,求出AD的值,作FS∥BC,利用平行线的性质得出AF=FS,根据等腰三角形的性质可以得出AH=HS,可以证明△FSG≌△EDG,FG=EG,通过计算可以求出GH=
AD.
(2)作EM⊥AD的延长线于M,由条件可以知道∠1=∠3,有∠2=∠3,AF=DE,可以证明Rt△AHF≌△EMD,得出FH=EM,进而可以得出△FHG≌△EMG,HG=GM,FG=GE,进而得出GH=
AD.
| 2 |
②)由条件可以求出AB=BD,AF=DE,从而得出∠BAD=∠BDA=60°,求出AD的值,作FR∥BC,利用平行线的性质得出AF=FR,根据等腰三角形的性质可以得出AH=HR,可以证明△FRG≌△EDG,FG=EG,通过计算可以求出GH=1.
③)由条件可以求出AB=BD,AF=DE,从而得出∠BAD=∠BDA=45°,求出AD的值,作FS∥BC,利用平行线的性质得出AF=FS,根据等腰三角形的性质可以得出AH=HS,可以证明△FSG≌△EDG,FG=EG,通过计算可以求出GH=
| 1 |
| 2 |
(2)作EM⊥AD的延长线于M,由条件可以知道∠1=∠3,有∠2=∠3,AF=DE,可以证明Rt△AHF≌△EMD,得出FH=EM,进而可以得出△FHG≌△EMG,HG=GM,FG=GE,进而得出GH=
| 1 |
| 2 |
解答: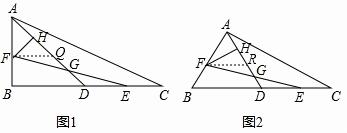 解:(1)①∵AD为边BC上的中线,
解:(1)①∵AD为边BC上的中线,
∴BD=DC=
BC,
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠BAD=∠BDA.
∵∠B=90°,
∴由勾股定理,得AD=2
,
作FQ∥BC,交AD于Q,
∴∠BDA=∠AQF,
∴∠BAD=∠AQF,
∴AF=FQ,
∵FH⊥AG,
∴AH=HQ,
∵CE=BF,
∴AF=DE,
∴△FQG≌△EDG,
∴FG=EG,QG=GD,
∵AH=HQ,
∴HG=
AD=
,
②∵AD为边BC上的中线,
∴BD=DC=
BC,
∵BC=2AB=4,
∴BD=DC=AB=2,
∵∠B=60°,
∴△AFR是等边三角形,
∴AD=2,
作FR∥BC,交AD于Q,
∴∠BDA=∠ARF,∠FGR=∠GDE,∠FGR=∠DGE,
∴∠BAD=∠ARF,
∴AF=FR,
∵FH⊥AG,
∴AH=HR,
∵CE=BF,
∴AF=DE,
∴△FRG≌△EDG,
∴FG=EG,RG=GD,
∵AH=HR,
∴HG=
AD=1,
③∵AD为边BC上的中线,
∴BD=DC=
BC,
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠BAD=∠BDA
作FS∥BC,交AD于Q,
∴∠BDA=∠ASF,∠FGS=∠GDE,∠FGS=∠DGE,
∴∠BAD=∠ASF,
∴AF=FS,
∵FH⊥AG,
∴AH=HS,
∵CE=BF,
∴AF=DE,
∴△FSG≌△EDG,
∴FG=EG,SG=GD,
∵AH=HS,
∴HG=
AD,
(2)∵AD为边BC上的中线,
∴BD=DC=
BC,
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3
∵CE=BF,
∴AF=ED,
作EM⊥AD的延长线于M,
∴∠M=90°,
∵FH⊥AG,
∴∠AHF=∠GHF=∠M=90°,
∴Rt△AHF≌△EMD
∴FH=EM,
∵∠FGH=∠EGM,
∴△FHG≌△EMG,
∴HG=GM,FG=GE
∵AD=DM+HD,
∴AD=DG+GM+HD,
∴AD=DG+HD+DG+HD,
∴AD=2(DG+HD)
∴AD=2HG
即HG=
AD.
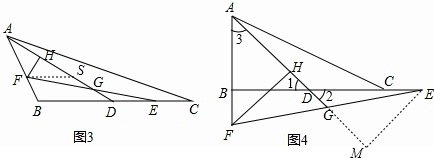
 解:(1)①∵AD为边BC上的中线,
解:(1)①∵AD为边BC上的中线,∴BD=DC=
| 1 |
| 2 |
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠BAD=∠BDA.
∵∠B=90°,
∴由勾股定理,得AD=2
| 2 |
作FQ∥BC,交AD于Q,
∴∠BDA=∠AQF,
∴∠BAD=∠AQF,
∴AF=FQ,
∵FH⊥AG,
∴AH=HQ,
∵CE=BF,
∴AF=DE,
∴△FQG≌△EDG,
∴FG=EG,QG=GD,
∵AH=HQ,
∴HG=
| 1 |
| 2 |
| 2 |
②∵AD为边BC上的中线,
∴BD=DC=
| 1 |
| 2 |
∵BC=2AB=4,
∴BD=DC=AB=2,
∵∠B=60°,
∴△AFR是等边三角形,
∴AD=2,
作FR∥BC,交AD于Q,
∴∠BDA=∠ARF,∠FGR=∠GDE,∠FGR=∠DGE,
∴∠BAD=∠ARF,
∴AF=FR,
∵FH⊥AG,
∴AH=HR,
∵CE=BF,
∴AF=DE,
∴△FRG≌△EDG,
∴FG=EG,RG=GD,
∵AH=HR,
∴HG=
| 1 |
| 2 |
③∵AD为边BC上的中线,
∴BD=DC=
| 1 |
| 2 |
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠BAD=∠BDA
作FS∥BC,交AD于Q,
∴∠BDA=∠ASF,∠FGS=∠GDE,∠FGS=∠DGE,
∴∠BAD=∠ASF,
∴AF=FS,
∵FH⊥AG,
∴AH=HS,
∵CE=BF,
∴AF=DE,
∴△FSG≌△EDG,
∴FG=EG,SG=GD,
∵AH=HS,
∴HG=
| 1 |
| 2 |
(2)∵AD为边BC上的中线,
∴BD=DC=
| 1 |
| 2 |
∵BC=2AB=4,
∴BD=DC=AB=2,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3
∵CE=BF,
∴AF=ED,
作EM⊥AD的延长线于M,
∴∠M=90°,
∵FH⊥AG,
∴∠AHF=∠GHF=∠M=90°,
∴Rt△AHF≌△EMD
∴FH=EM,
∵∠FGH=∠EGM,
∴△FHG≌△EMG,
∴HG=GM,FG=GE
∵AD=DM+HD,
∴AD=DG+GM+HD,
∴AD=DG+HD+DG+HD,
∴AD=2(DG+HD)
∴AD=2HG
即HG=
| 1 |
| 2 |

点评:本题考查了全等三角形的判定与性质,等腰直角三角形的性质,等腰三角形的角平分线、高、中线的性质,平行线的性质,勾股定理的运用.

练习册系列答案
相关题目
 20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B=
20、如图,在△ABC中,∠BAC=45°,现将△ABC绕点A逆时针旋转30°至△ADE的位置,使AC⊥DE,则∠B= 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为 2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( )
2、如图,在△ABC中,DE∥BC,那么图中与∠1相等的角是( ) 如图,在△ABC中,AB=AC,且∠A=100°,∠B=
如图,在△ABC中,AB=AC,且∠A=100°,∠B=