��Ŀ����
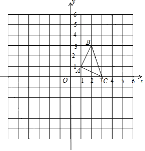
����Ŀ����ͼ1����֪����������A��B��Ӧ�����ֱ��ǩ�1��3����PΪ�����ϵ�һ���㣬���Ӧ����Ϊx

��1��A��B����ľ���AB=�� ����
��2�����������Ƿ���ڵ�P��ʹPA+PB=6�������ڣ������x��ֵ���������ڣ���˵�����ɣ�
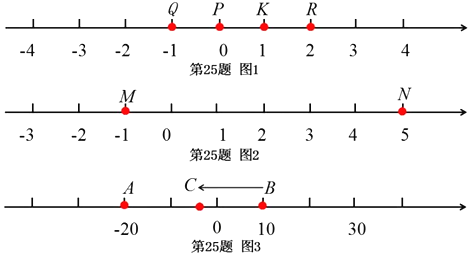
��3����ͼ2������P��ÿ��1����λ���ٶȴӵ�O���������˶���ͬʱ��A��ÿ��5����λ���ٶ������˶�����B��ÿ��20����λ���ٶ������˶������˶��Ĺ����У�M��N�ֱ���AP��OB���е㣬�ʣ�![]() ��ֵ�Ƿ����仯����˵�����ɣ�
��ֵ�Ƿ����仯����˵�����ɣ�
���𰸡���1��4����2����x=��1.5��3.5ʱ��PA+PB=5����3��![]() ��ֵ�������仯���������������
��ֵ�������仯���������������
��������
��1�����ݵ�A��B��Ӧ���������������ľ��빫ʽ�������AB�ij���
��2��������������ǣ��ٵ���P�ڵ�A���ʱ����PA+PB=5�ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ��ڵ���P�ڵ�A��B�м�ʱ����PA+PB=4��PA+PB=5��ͻ����ȥ���۵���P�ڵ�B�Ҳ�ʱ����PA+PB=5�ɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ�
��3�����˶�ʱ��Ϊt��ʱ���ҳ�OP��OA��OB�ij��ȣ������ɵó�AP�ij��ȣ���M��N�ֱ���AP��OB���е㣬�ɵó�AM��OM��MN�ij��ȣ��ٴ���![]() �м���������ۣ�
�м���������ۣ�
��1��A��B����ľ���AB=3������1��=4��
�ʴ�Ϊ��4��
��2��������������ǣ�
�ٵ���P�ڵ�A���ʱ��PA+PB=|x+1|+|x��3|=����x+1������x��3��=��2x+2=5��
��ã�x=��1.5��
�ڵ���P�ڵ�A��B�м�ʱ��PA+PB=4����ȥ����
�۵���P�ڵ�B�Ҳ�ʱ��PA+PB=|x+1|+|x��3|=��x+1��+��x��3��=2x��2=5��
��ã�x=3.5��
������������x=��1.5��3.5ʱ��PA+PB=5��
��3��![]() ��ֵ�������仯��
��ֵ�������仯��
�������£����˶�ʱ��Ϊt��ʱ����OP=t��OA=5t+1��OB=20t+3��
��AP=OA+OP=5t+1+t=6t+1��
��2AP=12t+2��
��M��N�ֱ���AP��OB���е㣬
��AM=![]() AP=3t+
AP=3t+![]() ��ON=
��ON=![]() OB=10t+
OB=10t+![]() ��
��
��OM=OA��AM=5t+1����3t+![]() ��=2t+
��=2t+![]() ��
��
��MN=OM+ON=2t+![]() +10t+
+10t+![]() =12t+2��
=12t+2��
��2AP =MN=12t+2��
��![]() ��ֵ�������仯��
��ֵ�������仯��

 ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д�
ӥ�ɽ̸��νӽ̲ĺӱ�����������ϵ�д� ���������ν�ϵ�д�
���������ν�ϵ�д�