题目内容
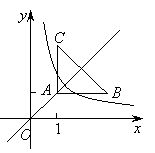
【题目】如图:等腰直角三角形ABC位于第一象限,AB=AC=2,直角顶点A在直线y=x上,其中A点的横坐标为1,且两条直角边AB、AC分别平行于x轴、y轴,若双曲线![]() (k≠0)与
(k≠0)与![]() 有交点,则k的取值范围是( )
有交点,则k的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
试题分析:直角顶点A在直线y=x上,易知A坐标(1,1),因为AB=AC=2,则B坐标(3,1);C坐标(1,3),且△ABC为等腰直角三角形,BC的中点坐标点E为(![]() ,
,![]() ),即为(2,2),
),即为(2,2),
∵点E(2,2)满足直线y=x。易知当双曲线与△ABC有唯一交点时,即双曲线与△ABC上交于极点A和极点E之间。根据A坐标判断k=1,E坐标判断k=4.所以,当双曲线与△ABC有唯一交点时k的取值范围为:1≤k≤4.

练习册系列答案
相关题目