题目内容
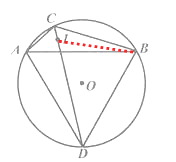
【题目】在⊙O 中,点C是![]() 上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
上的一个动点(不与点A,B重合),∠ACB=120°,点I是∠ABC的内心,CI的延长线交⊙O于点D,连结AD,BD.
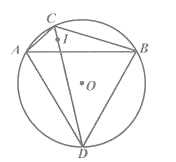
(1)求证:AD=BD.
(2)猜想线段AB与DI的数量关系,并说明理由.
(3)若⊙O的半径为2,点E,F是![]() 的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
的三等分点,当点C从点E运动到点F时,求点I随之运动形成的路径长.
【答案】(1)证明见解析;(2)AB=DI,理由见解析(3)![]()
【解析】(1)根据内心的定义可得CI平分∠ACB,可得出角相等,再根据圆周角定理,可证得结论;
(2)根据∠ACB=120°,∠ACD=∠BCD,可求出∠BAD的度数,再根据AD=BD,可证得△ABD是等边三角形,再根据内心的定义及三角形的外角性质,证明∠BID=∠IBD,得出ID=BD,再根据AB=BD,即可证得结论;
(3)连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧,根据已知及圆周角定理、解直角三角形,可求出AD的长,再根据点E,F是 弧AB 的三等分点,△ABD是等边三角形,可证得∠DAI1=∠AI1D,然后利用弧长的公式可求出点I随之运动形成的路径长.
(1)证明:∵点I是∠ABC的内心
∴CI平分∠ACB
∴∠ACD=∠BCD
∴弧AD=弧BD
∴AD=BD
(2)AB=DI
理由:∵∠ACB=120°,∠ACD=∠BCD
∴∠BCD=![]() ×120°=60°
×120°=60°
∵弧BD=弧BD
∴∠DAB=∠BCD=60°
∵AD=BD
∴△ABD是等边三角形,
∴AB=BD,∠ABD=∠C
∵I是△ABC的内心
∴BI平分∠ABC
∴∠CBI=∠ABI
∵∠BID=∠C+∠CBI,∠IBD=∠ABI+∠ABD
∴∠BID=∠IBD
∴ID=BD
∵AB=BD
∴AB=DI
(3)解:如图,连接DO,延长DO根据题意可知点I随之运动形成的图形式以D为圆心,DI1为半径的弧

∵∠ACB=120°,弧AD=弧BD
∴∠AED=![]() ∠ACB=
∠ACB=![]() ×120°=60°
×120°=60°
∵圆的半径为2,DE是直径
∴DE=4,∠EAD=90°
∴AD=sin∠AED×DE=![]() ×4=2
×4=2![]()
∵点E,F是 弧AB 的三等分点,△ABD是等边三角形,
∴∠ADB=60°
∴弧AB的度数为120°,
∴弧AM、弧BF的度数都为为40°
∴∠ADM=20°=∠FAB
∴∠DAI1=∠FAB+∠DAB=80°
∴∠AI1D=180°-∠ADM-∠DAI1=180°-20°-80°=80°
∴∠DAI1=∠AI1D
∴AD=I1D=2![]()
∴弧I1I2的长为:![]()