题目内容
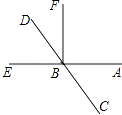
【题目】如图,点O是直线EF上一点,射线OA,OB,OC在直线EF的上方,射线OD的直线EF的下方,且OF平分∠COD,OA⊥OC,OB⊥OD. 
(1)若∠DOF=25°,求∠AOB的度数.
(2)若OA平分∠BOE,则∠DOF的度数是 . (直接写出答案)
【答案】
(1)解:∵∠DOF=25°,OF平分∠COD,
∴∠DOC=50°,
∵OB⊥OD,
∴∠BOC=90°﹣50°=40°,
∵OA⊥OC,
∴∠AOB=90°﹣∠BOC=50°
(2)30°
【解析】解:(2)∵∠BOC+∠COD=90°,∠AOB+∠BOC=90°,
∴∠COD=∠AOB,
设∠DOF=∠COF=x,
∵OA平分∠BOE,
∴∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,
∴5x+90°﹣2x=180°,
解得:x=30°,
即∠DOF=30°.
故答案为:30°.
(1)利用角平分线的定义可得∠DOC=50°,由垂直的定义可得∠BOD=90°,易得∠BOC=40°,因为OA⊥OC,可得结果;(2)利用垂直的定义易得∠BOC+∠COD=90°,∠AOB+∠BOC=90°,可得∠COD=∠AOB,设∠DOF=∠COF=x,利用平分线的定义可得∠AOE=∠AOB=∠COD=2x,∠BOC=90°﹣2x,由平角的定义可得5x+90°﹣2x=180°,解得x,即得结果.

练习册系列答案
相关题目
【题目】表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数x与方差s2,根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
甲 | 乙 | 丙 | 丁 | |
平均数x/cm | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
A.甲B.乙C.丙D.丁