题目内容
【题目】如图1,已知点E和点F分别在直线AB和CD上,EL和FG分别平分∠BEF和∠EFC,EL∥FG.
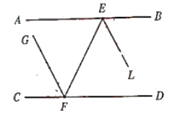
(1)求证:AB∥CD;
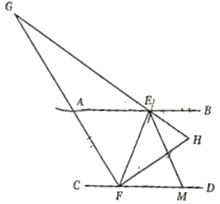
(2)如图,点M为FD上一点,∠BEM,∠EFD的角平分线EH,FH相交于点H,若∠H=∠FEM+15°,延长HE交FG于G点,求∠G的度数;
(3)如图,点N在直线AB和直线CD之间,且EN⊥FN,点P为直线AB上的点,若∠EPF,∠PFN的角平分级交于点Q,设∠BEN=α,直接写出∠PQF的大小为(用含α的式子表示).
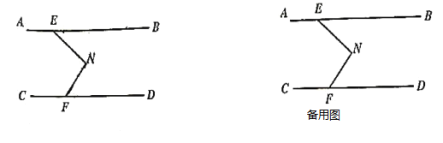
【答案】(1)见解析; (2)∠G=25°;(3) 135°-![]() 或135°+
或135°+![]() .
.
【解析】
(1)首先根据角平分线可得∠BEL=∠FEL,∠CFG=∠EFG,再根据EL∥FG,结合可证明∠CFE=∠BEF,进而证明AB∥CD.
(2)根据设元导角结合平行线的性质即可求得∠G.
(3)首先根据题意要分类讨论,第一种情况当点P在E点左侧;第二种情况当点P在EH之间;第三种情况当点P在H点右侧.
(1)证明:
∵EL和FG分别平分∠BEF和∠EFC
∴∠BEL=∠FEL,∠CFG=∠EFG
又∵EL∥FG
∴∠EFG=∠FEL
∴∠CFG=∠EFG=∠FEL=∠BEL,
∠CFG+∠EFG=∠FEL+∠BEL
即∠CFE=∠BEF
∴AB∥CD
(2)提示:(注意:模型和△导角均需通过平行线导角进一步证明)
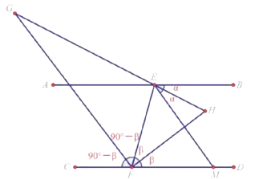
如图设元导角
臭脚模型:∠G=∠BEG-∠DFG
=180°-α-(90°+β)
=90°-(α+β)
猪蹄模型:∠H=α+β
∵AB∥CD
∴2α+∠FEM+∠B=180°
∴∠FEM=180°-2β-2a
∵∠H=∠FEM+15°
∴a+β=180×-2β-2α+15°
解得,α+β=65°
∴∠G=90°-(α+β)=25°
(3) 135°-![]() 或135°+
或135°+![]()
延长FN交直线AB于H点.
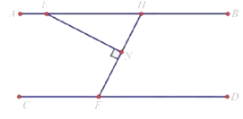
①当点P在E点左侧时,如图设元导角△PQF内角和:

∠PQF=180°-x-y
猪蹄模型:
∠DFN=∠N-∠BEN=90°-α
∵AB∥CD
∴2x+2y+90°-α=180°
∴x+y=45°+![]()
∴∠PQF=180°-(45°+![]() )=135°-
)=135°-![]()
②当点P在EH之间时,如图,此时点Q在CEPF的角平分线的反向延长线与∠PFN的角平分线交点处,不合题意,舍去。


③当点P在H点右侧时,如图设元导角
△PQF内角和:
∠PQF=180°-x-y
∵AB∥CD
∴∠APF=∠DFP=2x
猪蹄模型:α+2y+2x=90°
∴x+y=45°-![]()
∴∠PQF=180°-(45°-![]() )=135°+
)=135°+![]()
综上:∠PQF=135°-![]() 或135+
或135+![]()

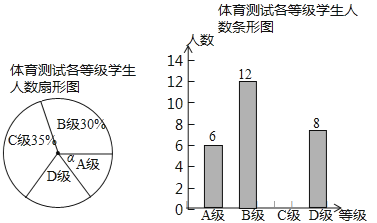
【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率