题目内容
 11、如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )
11、如图,AB∥CD,AC∥BD,AD与BC交于O,AE⊥BC于E,DF⊥BC于F,那么图中全等的三角形有( )分析:根据题意,结合图形,图中全等的三角形有△AOE≌△DOF,△CAB≌△CDB,△AOB≌△COD,△AOC≌△BOD,△AEC≌△BFD,△AEB≌△DFC,△ACD≌△DBA做题时要从已知条件开始结合图形利用全等的判定方法由易到难逐个寻找.
解答:解:∵AB∥CD,AC∥BD,
∴∠ABC=∠DCB,∠ACB=∠DBC.
∵BC=CB,
∴△CAB≌△CDB,
∴AB=CD,AC=BD.
∵AB∥CD,AC∥BD,
∴∠BAO=∠CDO,∠OBA=∠OCD,∠OBD=∠OCA,∠OAC=∠ODB.
∴△AOB≌△COD,△AOC≌△BOD.
∴OA=OD,OC=OB.
∵AE⊥BC,DF⊥BC,∠AOE=∠DOF,
∴△AOE≌△DOF.
∴OE=OF.
∴CE=BF.
∵AE=DF,AC=BD,
∴△AEC≌△BFD.
∵AE=DF,AB=CD,BE=CF,
∴△AEB≌△DFC.
还有△ACD≌△DBA.
故选C.
∴∠ABC=∠DCB,∠ACB=∠DBC.
∵BC=CB,
∴△CAB≌△CDB,
∴AB=CD,AC=BD.
∵AB∥CD,AC∥BD,
∴∠BAO=∠CDO,∠OBA=∠OCD,∠OBD=∠OCA,∠OAC=∠ODB.
∴△AOB≌△COD,△AOC≌△BOD.
∴OA=OD,OC=OB.
∵AE⊥BC,DF⊥BC,∠AOE=∠DOF,
∴△AOE≌△DOF.
∴OE=OF.
∴CE=BF.
∵AE=DF,AC=BD,
∴△AEC≌△BFD.
∵AE=DF,AB=CD,BE=CF,
∴△AEB≌△DFC.
还有△ACD≌△DBA.
故选C.
点评:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
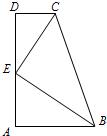 23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.
23、如图,AB∥CD,∠A=90°,AB=2,BC=3,CD=1,E是AD中点.求证:CE⊥BE.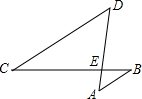 如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=
如图,AB∥CD,AD与BC相交于点E,如果AB=2,CD=6,AE=1,那么DE=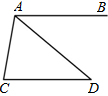 4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( )
4、如图,AB∥CD,∠C=80°,∠CAD=60°,则∠BAD的度数等于( ) 34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.
34、如图,AB∥CD,P是BC上的一个动点,设∠CDP=∠1,∠CPD=∠2,请你猜想出∠1、∠2与∠B之间的关系,并说明理由.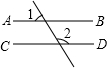 如图,AB∥CD,∠1=58°,则∠2的度数是( )
如图,AB∥CD,∠1=58°,则∠2的度数是( )