题目内容
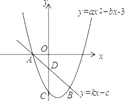
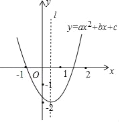
【题目】如图，抛物线y＝ax2+bx+c经过点（﹣1，0），对称轴为直线l，则下列结论：①abc＞0；②a+b+c＞0；③a+c＞0；④a+b＞0，正确的是（ ）
A. ①②④B. ②④C. ①③D. ①④
【答案】D
【解析】
由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴进行推理，进而对所得结论进行判断．
解：①抛物线的对称轴位于y轴的右侧，则a、b异号，即ab＜0．
抛物线与y轴交于负半轴，则c＜0．
所以abc＞0．
故正确；
②如图所示，当x＝1时，y＜0，即a+b+c＜0，
故错误；
③由图可知，当x＝﹣1时，y＝0，即a﹣b+c＝0，
x＝1时，y＜0，即a+b+c＜0，
所以 a+a+c+c＜0．
所以 2a+2c＜0．
所以 a+c＜0．
故错误；
④由图可知，当x＝﹣1时，y＝0，即a﹣b+c＝0．
当x＝2时，y＞0，即4a+2b+c＞0，
所以 4a+2b+b﹣a＞0，
所以 3a+3b＞0．
所以 a+b＞0．
故正确．
故选：D．
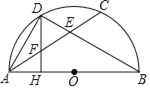
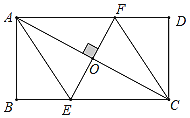
【题目】如图，矩形ABCD的对角线AC的中点为O，过点O作
，交BC边于点E，交AD边于点F，分别连接AE、CF．
（1）求证：四边形AECF是菱形；
（2）若
，
，请直接写出EF的长为__________．
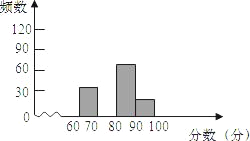
【题目】某校举行手工制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x＜100 | 20 | 0.1 |
请根据以上图表提供的信息，解答下列问题：
（1）表中m和n所表示的数分别为：m＝______，n＝______，
（2）请在图中，补全频数分布直方图；
（3）比赛成绩的中位数落在哪个分数段？
（4）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？
