题目内容
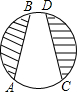
如图是某公园的一角,∠AOB=90°,弧AB的半径OA长是6米,C是OA的中点,点D在弧AB上,CD∥OB,则图中休闲区(阴影部分)的面积是______.
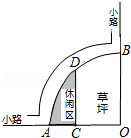

如图,连接OD.
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
OA=
×6=3米,
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,∵OD=6,OC=3,
∴CD=
=
=3
米,
∵sin∠DOC=
=
=
,
∴∠DOC=60°,
∴S阴影=S扇形AOD-S△DOC=
-
×3×3
=6π-
(平方米).
故答案是:6π-
.
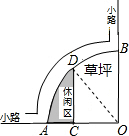
∵弧AB的半径OA长是6米,C是OA的中点,
∴OC=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠AOB=90°,CD∥OB,
∴CD⊥OA,
在Rt△OCD中,∵OD=6,OC=3,
∴CD=
| OD2-OC2 |
| 62-32 |
| 3 |
∵sin∠DOC=
| CD |
| OD |
3
| ||
| 6 |
| ||
| 2 |
∴∠DOC=60°,
∴S阴影=S扇形AOD-S△DOC=
| 60×π×62 |
| 360 |
| 1 |
| 2 |
| 3 |
| 9 |
| 2 |
| 3 |
故答案是:6π-
| 9 |
| 2 |
| 3 |


练习册系列答案
相关题目