题目内容
如图,△ABC中,AE交BC于点D,∠C=∠E,AD=4,BC=8,BD:DC=5:3,则DE的长等于( )
A. | B. | C. | D. |
D.
解析试题分析:在△BDE和△ADC中,
∠C=∠E,∠BDE=∠ADC
∴△BDE∽△ADC
∴
∵BC=8,BD:DC=5:3,
∴BD=5,CD=3
∴DE=
故选D.
考点:相似三角形的判定与性质.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
如图,△ABC为等腰直角三角形,∠BAC=90°,BC=2,E为AB上任意一动点,以CE为斜边作等腰Rt△CDE,连接AD,下列说法:
①∠BCE=∠ACD;②AC⊥ED;③△AED∽△ECB;④AD∥BC;⑤四边形ABCD的面积有最大值,且最大值为 .其中,正确的结论是 。
.其中,正确的结论是 。
| A.①②④ | B.①③⑤ | C.②③④ | D.①④⑤ |

如图,在平行四边形ABCD中,AC与BD交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF∶FC=
| A.1∶4 | B.1∶3 | C.2∶3 | D.1∶2 |
如图,在△ABC中,若DE∥BC,AD=5,BD=10,DE=4,则BC的值为( )
| A.8 | B.9 | C.10 | D.12 |
如图,在△ABC中,AD,BE是两条中线,则S△EDC∶S△ABC= ( )
| A.1∶2 | B.2∶3 |
| C.1∶3 | D.1∶4 |
如图,在△ 中,
中, 为
为 边上一点,∠
边上一点,∠ ∠
∠ ,
, ,
, ,则
,则 的长为( )
的长为( )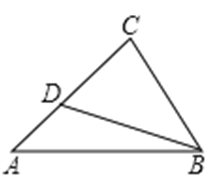
| A.1 | B.4 | C.3 | D.2 |

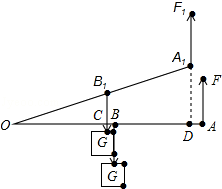
 ,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )
,若点A′的坐标为(1,2),则正方形A′B′C′D′与正方形ABCD的相似比是( )



