题目内容
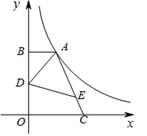
如图1和2,在△ABC中,AB=13,BC=14,cos∠ABC= .
.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积S△ABC= ;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为S△ABD=0)
(1)用含x,m,n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.
 .
.探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积S△ABC= ;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A、C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为S△ABD=0)
(1)用含x,m,n的代数式表示S△ABD及S△CBD;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,指出这样的x的取值范围.
发现:请你确定一条直线,使得A、B、C三点到这条直线的距离之和最小(不必写出过程),并写出这个最小值.

探究:12;15;84
拓展:(1)
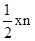
(2)当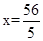 时,
时, 的最大值为15,当
的最大值为15,当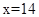 时,
时, 的最小值为12
的最小值为12
(3)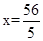 或
或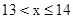
发现:直线AC,A、B、C三点到这条直线的距离之和最小,最小值为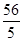
拓展:(1)

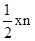
(2)当
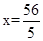 时,
时, 的最大值为15,当
的最大值为15,当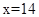 时,
时, 的最小值为12
的最小值为12(3)
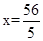 或
或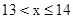
发现:直线AC,A、B、C三点到这条直线的距离之和最小,最小值为
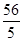
探究:在Rt△ABH中,AB=13,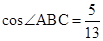 ,∴BH=AB
,∴BH=AB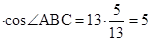 。
。
∴根据勾股定理,得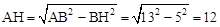 。
。
∵BC=14,∴HC=BC-BH=9。∴根据勾股定理,得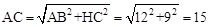 。
。
∴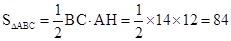 。
。
拓展:(1)直接由三角形面积公式可得。
(2)由(1)和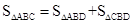 即可得到
即可得到 关于x的反比例函数关系式。根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大。从而根据反比例函数的性质求出m+n)的最大值和最小值。
关于x的反比例函数关系式。根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大。从而根据反比例函数的性质求出m+n)的最大值和最小值。
(3)当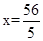 时,此时BD⊥AC,在线段AC上存在唯一的点D;当
时,此时BD⊥AC,在线段AC上存在唯一的点D;当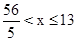 时,此时在线段AC上存在两点D;当
时,此时在线段AC上存在两点D;当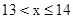 时,此时在线段AC上存在唯一的点D。因此x的取值范围为
时,此时在线段AC上存在唯一的点D。因此x的取值范围为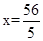 或
或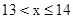 。
。
发现:由拓展(2)知,直线AC,A、B、C三点到这条直线的距离之和(即△ABC中AC边上的高)最小,最小值为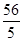 (它小于BC边上的高12和AB边上的高
(它小于BC边上的高12和AB边上的高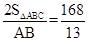 )。
)。
解:探究:12;15;84。
拓展:(1)由三角形面积公式,得
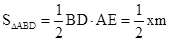 ,
,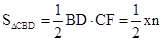 。
。
(2)由(1)得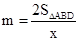 ,
,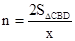 ,
,
∴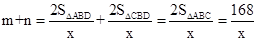
∵△ABC中AC边上的高为 ,
,
∴x的取值范围为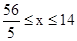 。
。
∵ 随x的增大而减小,
随x的增大而减小,
∴当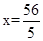 时,
时, 的最大值为15,当
的最大值为15,当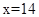 时,
时, 的最小值为12。
的最小值为12。
(3)x的取值范围为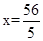 或
或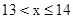 。
。
发现:直线AC,A、B、C三点到这条直线的距离之和最小,最小值为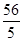 。
。
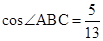 ,∴BH=AB
,∴BH=AB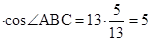 。
。∴根据勾股定理,得
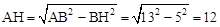 。
。∵BC=14,∴HC=BC-BH=9。∴根据勾股定理,得
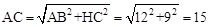 。
。∴
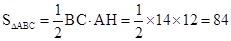 。
。拓展:(1)直接由三角形面积公式可得。
(2)由(1)和
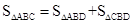 即可得到
即可得到 关于x的反比例函数关系式。根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大。从而根据反比例函数的性质求出m+n)的最大值和最小值。
关于x的反比例函数关系式。根据垂直线段最短的性质,当BD⊥AC时,x最小,由面积公式可求得;因为AB=13,BC=14,所以当BD=BC=14时,x最大。从而根据反比例函数的性质求出m+n)的最大值和最小值。(3)当
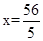 时,此时BD⊥AC,在线段AC上存在唯一的点D;当
时,此时BD⊥AC,在线段AC上存在唯一的点D;当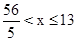 时,此时在线段AC上存在两点D;当
时,此时在线段AC上存在两点D;当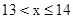 时,此时在线段AC上存在唯一的点D。因此x的取值范围为
时,此时在线段AC上存在唯一的点D。因此x的取值范围为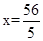 或
或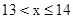 。
。发现:由拓展(2)知,直线AC,A、B、C三点到这条直线的距离之和(即△ABC中AC边上的高)最小,最小值为
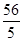 (它小于BC边上的高12和AB边上的高
(它小于BC边上的高12和AB边上的高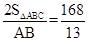 )。
)。解:探究:12;15;84。
拓展:(1)由三角形面积公式,得
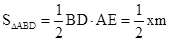 ,
,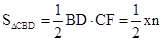 。
。(2)由(1)得
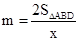 ,
,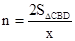 ,
,∴
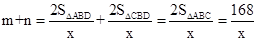
∵△ABC中AC边上的高为
 ,
,∴x的取值范围为
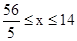 。
。∵
 随x的增大而减小,
随x的增大而减小,∴当
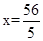 时,
时, 的最大值为15,当
的最大值为15,当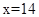 时,
时, 的最小值为12。
的最小值为12。(3)x的取值范围为
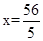 或
或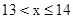 。
。发现:直线AC,A、B、C三点到这条直线的距离之和最小,最小值为
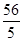 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的函数叫做“奇特函数”.当
的函数叫做“奇特函数”.当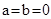 时,“奇特函数”
时,“奇特函数”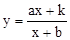 就是反比例函数
就是反比例函数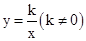 .
.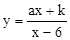 的图象经过B,E两点.
的图象经过B,E两点. 的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为
的图象向右平移6个单位,再向上平移 个单位就可得到①中所得“奇特函数”的图象.过线段BE中点M的一条直线l与这个“奇特函数”的图象交于P,Q两点,若以B、E、P、Q为顶点组成的四边形面积为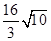 ,请直接写出点P的坐标.
,请直接写出点P的坐标.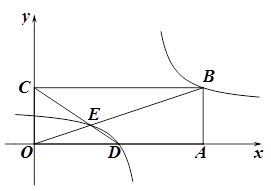
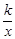 的图像交BC、AB于点D、E.
的图像交BC、AB于点D、E.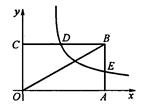
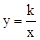 的图像经过A(-2,3),则当
的图像经过A(-2,3),则当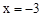 时,y的值是 .
时,y的值是 .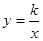 和
和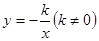 的图象关于y轴对称,我们定义函数
的图象关于y轴对称,我们定义函数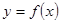 和
和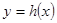 的图象关于y轴对称,那么我们定义函数
的图象关于y轴对称,那么我们定义函数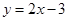 的“影像”函数: ;
的“影像”函数: ;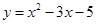 ;
;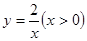 和
和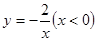 的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数
的图象分别交于点A、B、C(点A、B在第一象限),如果CB: BA=1:2,点C在函数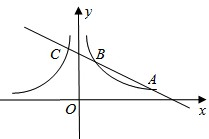
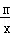 的图象如图,以下结论:
的图象如图,以下结论: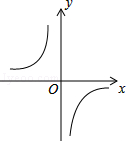
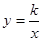 的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
的第一象限的那一支上,AB⊥y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .