题目内容
 如图,直线y=kx(k>0)与双曲线y=
如图,直线y=kx(k>0)与双曲线y= 交于A(a,b),B(c,d)两点,则3ad-5bc=________.
交于A(a,b),B(c,d)两点,则3ad-5bc=________.
6
分析:本题需先根据交点的性质,把A(a,b),B(c,d)分别代入直线y=kx(k>0)与双曲线y= 中,求出它们之间相等的量,最后再把他们代入及可求出结果.
中,求出它们之间相等的量,最后再把他们代入及可求出结果.
解答:∵直线y=kx(k>0)与双曲线y= 交于A(a,b),B(c,d)两点,
交于A(a,b),B(c,d)两点,
∴把A(a,b),B(c,d)代入上式得;
k= ,k=
,k=
∴
∴ad=bc
∵ab=3,cd=3
∴abcd=9,即(ad)2=9,
∴ad=bc=-3,
∴3ad-5bc=-9+15=6.
故答案为6.
点评:本题主要考查了反比例函数与一次函数的交点问题,在解题时要注意交点与函数的性质问题.
分析:本题需先根据交点的性质,把A(a,b),B(c,d)分别代入直线y=kx(k>0)与双曲线y=
 中,求出它们之间相等的量,最后再把他们代入及可求出结果.
中,求出它们之间相等的量,最后再把他们代入及可求出结果.解答:∵直线y=kx(k>0)与双曲线y=
 交于A(a,b),B(c,d)两点,
交于A(a,b),B(c,d)两点,∴把A(a,b),B(c,d)代入上式得;
k=
 ,k=
,k=
∴

∴ad=bc
∵ab=3,cd=3
∴abcd=9,即(ad)2=9,
∴ad=bc=-3,
∴3ad-5bc=-9+15=6.
故答案为6.
点评:本题主要考查了反比例函数与一次函数的交点问题,在解题时要注意交点与函数的性质问题.

练习册系列答案
相关题目
 如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )
如图,直线y=kx+b经过点A(0,3),B(-2,0),则k的值为( )| A、3 | ||
B、
| ||
C、
| ||
D、-
|
 如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式
如图,直线y=kx+b经过A(2,1),B(-1,-2)两点,则不等式| 1 |
| 2 |
| A、x<2 |
| B、x>-1 |
| C、x<1或x>2 |
| D、-1<x<2 |
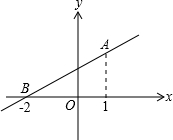 如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为
如图,直线y=kx+b经过A(1,2)和B(-2,0)两点,则不等式组-x+3≥kx+b>0的解集为 7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( )
7、如图,直线y=kx+b和y=mx都经过点A(-1,-2),则不等式mx<kx+b的解集为( ) 16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为
16、如图,直线y=kx-1经过点(2,1),则不等式0≤x<2kx+2的解集为