题目内容
如图,点D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.
求证:BD平分∠ABC.
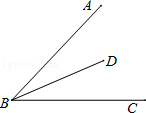
求证:BD平分∠ABC.

证明见解析.
试题分析:在AB上截取ME=BN,证得△BND≌△EMD,进而证得∠DBN=∠MED,BD=DE,从而证得BD平分∠ABC.
试题解析:如图所示:在AB上截取ME=BN,

∵∠BMD+∠DME=180°,∠BMD+∠BND=180°,
∴∠DME=∠BND,
在△BND与△EMD中,
 ,
,∴△BND≌△EMD(SAS),
∴∠DBN=∠MED,BD=DE,
∴∠MBD=∠MED,
∴∠MBD=∠DBN,
∴BD平分∠ABC.
【考点】1.全等三角形的判定与性质;2.角平分线的性质.

练习册系列答案
相关题目