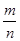题目内容
某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据: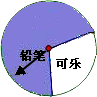
(1)计算并完成表格:
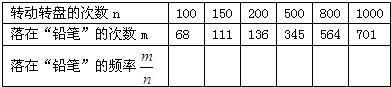
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 | ||
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 | ||
落在“铅笔”的频率
|
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
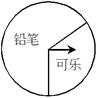
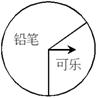
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少?(精确到1°)
分析:(1)根据频率的算法,频率=
,可得各个频率;填空即可;
(2)根据频率的定义,可得当n很大时,频率将会接近其概率;
(3)根据概率的求法计算即可;
(4)根据扇形图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可.
| 频数 |
| 总数 |
(2)根据频率的定义,可得当n很大时,频率将会接近其概率;
(3)根据概率的求法计算即可;
(4)根据扇形图中,每部分占总体的百分比等于该部分所对应的扇形圆心角的度数与360°的比计算即可.
解答:解:(1)
(2)当n很大时,频率将会接近(68+111+136+345+564+701)÷(100+150+200+500+800+1000)≈0.7;
(3)获得铅笔的概率约是0.7;
(4)扇形的圆心角约是0.7×360°=252度.
| 转动转盘的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 落在“铅笔”的次数m | 68 | 111 | 136 | 345 | 564 | 701 |
| 落在“铅笔”的频率 | 0.68 | 0.74 | 0.68 | 0.69 | 0.705 | 0.701 |
(3)获得铅笔的概率约是0.7;
(4)扇形的圆心角约是0.7×360°=252度.
点评:本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.用到的知识点为:频率=所求情况数与总情况数之比.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
某商场设立了一个可以自由转动的转盘,并规定:顾客购物10元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是活动进行中的一组统计数据:
(1)计算并完成表格:
(2)请估计,当n很大时,频率将会接近多少?
(3)假如你去转动该转盘一次,你获得铅笔的概率约是多少?
(4)在该转盘中,表示“铅笔”区域的扇形的圆心角约是多少(精确到1°)
|
转动转盘的次数n |
100 |
150 |
200 |
500 |
800 |
1000 |
|
落在“铅笔”的次数m |
68 |
111 |
136 |
345 |
564 |
701 |
|
落在“铅笔”的频率 |
|
|
|
|
|
|
(在下面的23、24两题中任选做一题,若两题都答,按23题评分)