题目内容
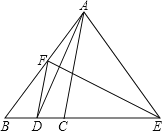
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.
【答案】见解析
【解析】
(1)由EF是AD的垂直平分线可得AE=DE,由此即可得到∠EAD=∠EDA;
(2)由EF是AD的垂直平分线可得AF=DF,由此可得∠FAD=∠FDA,由AD平分∠BAC可得∠FAD=∠CAD,从而可得∠FDA=∠CAD,由此即可得到DF∥AC;
(3)由三角形外角的性质可得∠EAC=∠EAD-∠CAD,∠B=∠EDA-∠BAD结合∠EAD=∠EDA,∠BAD=∠CAD即可得到∠EAC=∠B.
(1)∵ EF是AD的垂直平分线,
∴AE=DE,
∴∠EAD=∠EDA;
(2)∵ EF是AD的垂直平分线,
∴AF=DF,
∴∠FAD=∠FDA,
∵AD是∠BAC平分线,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF//AC;
(3)∵∠EAC=∠EAD -∠CAD,∠B=∠EDA -∠BAD,∠BAD=∠CAD,∠EAD=∠EDA,
∴∠EAC=∠B.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目