题目内容
【题目】如图,已知![]() ,
,![]() ,
,![]() ,
,![]() .
.![]() 是射线
是射线![]() 上的动点(点
上的动点(点![]() 与点
与点![]() 不重合),
不重合),![]() 是线段
是线段![]() 的中点,连结
的中点,连结![]() ,交线段
,交线段![]() 于点
于点![]() ,如果以
,如果以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,则线段
相似,则线段![]() 的长为________.
的长为________.

【答案】![]() 或
或![]()
【解析】
如果△ADN和△BME相似,一定不相等的角是∠ADN和∠MBE,因为AD∥BC,如果两角相等,那么M与D重合,显然不合题意.因此本题分①当∠ADN=∠BME时和②当∠AND=∠BEM时,两种情况解答即可.
因为如果△ADN和△BME相似,一定不相等的角是∠ADN和∠MBE,因为AD∥BC,如果两角相等,那么M与D重合,显然不合题意,故应分两种情况进行讨论.
图1,当∠ADN=∠BEM时,那么∠ADB=∠BEM,∴tan∠ADB=tan∠BEM.
作DF⊥BE,垂足为F,可得四边形ABFD为矩形,则AB=DF,设BE=x,

∵tan∠ADB= AB:AD,tan∠BEM =DF:FE,
∴AB:AD=DF:FE=AB:(BE-AD).
即2:4=2:(x-4).
解得x=8.
即BE=8.
②如图2,当∠ADB=∠BME,
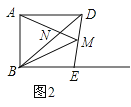
而∠ADB=∠DBE,
∴∠DBE=∠BME,
∵∠E是公共角,
∴△BED∽△MEB,
∴![]() ,即BE2=DEEM,
,即BE2=DEEM,
∵M是线段DE的中点,
∴EM=![]() DE,
DE,
设BE=x,结合图1,根据勾股定理可得:![]()
∴![]() =
= ![]() [22+(x-4)2],
[22+(x-4)2],
∴x1=2,x2=-10(舍去),
∴BE=2.
综上,线段BE的长为8或2,
故答案为8或2.

【题目】在不透明的袋子中有黑棋子10枚和白棋子若干(它们除颜色外都相同),现随机从中摸出10枚记下颜色后放回,这样连续做了10次,记录了如下的数据:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
黑棋数 | 1 | 3 | 0 | 2 | 3 | 4 | 2 | 1 | 1 | 3 |
根据以上数据,估算袋中的白棋子数量为( )
A. 60枚 B. 50枚 C. 40枚 D. 30枚








