题目内容
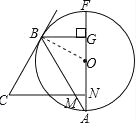
【题目】如图,CB是⊙O的切线,AF是⊙O的直径,CN⊥AF于点N,BG⊥AF于点G,连接AB交CN于点M.
(1)写出与点B有关的三条不同类型的结论.(2)、若AG=3FG,求tanA的值.

【答案】(1)、OB⊥BC,AB⊥BF,OA=OB,BC=CM;(2)、![]() .
.
【解析】
试题分析:(1)、由切线的性质和圆的性质即可得出结论;(2)、连接OB,由AG=3FG,推出FG=OG=![]() OF,得到OG=
OF,得到OG=![]() OB,根据直角三角形的性质得到∠GBO=30°,即可求得∠A=
OB,根据直角三角形的性质得到∠GBO=30°,即可求得∠A=![]() =30°,于是得到结果.
=30°,于是得到结果.
试题解析:(1)、与点B有关的结论:OB⊥BC,AB⊥BF,OA=OB,BC=CM;
(2)、如图,连接OB,∵AG=3FG,∴FG=OG=![]() OF,∴OG=
OF,∴OG=![]() OB,∵BG⊥AF,∴∠GBO=30°,
OB,∵BG⊥AF,∴∠GBO=30°,
∴∠BOG=60°,∵OB=OA,∴∠A=![]() =30°,∴tan∠A=
=30°,∴tan∠A=![]() .
.

练习册系列答案
相关题目