题目内容
直角三角形两直角边的长分别为3和4,则连接这两条直角边的中点的线段长为
- A.1.5
- B.2
- C.2.5
- D.5
C
分析:易求得直角三角形的斜边长,那么所求的线段为三角形的中位线等于该三角形斜边的一半.
解答:∵直角三角形两直角边的长分别为3和4,
∴斜边为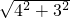 =5,
=5,
又∵连接这两条直角边的中点的线段是三角形的中位线,
∴线段长为 ×5=2.5,
×5=2.5,
故选C.
点评:本题考查的是三角形中位线的定义和性质以及勾股定理的运用,是中学阶段的常规题.
分析:易求得直角三角形的斜边长,那么所求的线段为三角形的中位线等于该三角形斜边的一半.
解答:∵直角三角形两直角边的长分别为3和4,
∴斜边为
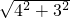 =5,
=5,又∵连接这两条直角边的中点的线段是三角形的中位线,
∴线段长为
 ×5=2.5,
×5=2.5,故选C.
点评:本题考查的是三角形中位线的定义和性质以及勾股定理的运用,是中学阶段的常规题.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
已知一直角三角形两直角边的长分别是3cm和4cm,以直角顶点为圆心,2.4cm长为半径作⊙O,则⊙O与斜边的位置关系是( )
| A、相交 | B、相切 | C、相离 | D、以上都不对 |
已知直角三角形两直角边的边长之和为
,斜边长为2,则这个三角形的面积是( )
| 6 |
A、
| ||
B、
| ||
| C、1 | ||
D、2
|
已知直角三角形两直角边的边长之和为
,斜边长为2,则这个三角形的面积是( )
| 6 |
| A、0.25 | ||
| B、0.5 | ||
| C、1 | ||
D、2
|