题目内容
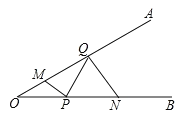
【题目】如图,∠AOB=30°,M、N分别在OA、OB上,且OM=2,ON=4,点P、Q分别在OB、OA上,则MP+PQ+QN的最小值是 _______.
【答案】2![]()
【解析】
作M关于OB的对称点M',作N关于OA的对称点N',连接M'N',可以得出M'N'即为MP+PQ+QN的最小值;证出△ONN'为等边三角形,△OMM'为等边三角形,得出∠N'OM'=90°,由勾股定理求出M'N'即可.
作M关于OB的对称点M',作N关于OA的对称点N',如图所示:
连接M'N'交OB于点P,交OA于点Q,连接MP,PQ,QN,则MP+PQ+QN=M'P+PQ+QN'=M'N',∴M'N'为MP+PQ+QN的最小值.
根据轴对称的定义可知:∠N'OQ=∠M'OB=30°,∠ONN'=60°,∴△ONN'为等边三角形,△OMM'为等边三角形,∴∠N'OM'=90°ON'=ON=4,OM'=OM=2,∴在Rt△M'ON'中,M'N'![]() .
.
故答案为:2![]() .
.


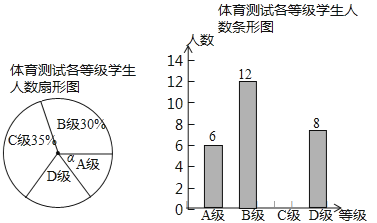
【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

【题目】某学习小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如下的表格,则符合这一结果的实验最有可能的是( )
实验次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 2000 |
频率 | 0.365 | 0.328 | 0.330 | 0.334 | 0.336 | 0.332 | 0.333 |
A.一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
B.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
C.抛一个质地均匀的正六面体骰子,向上的面点数是5
D.抛一枚硬币,出现反面的概率