题目内容
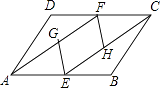
【题目】如图,在ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连结AF,CE,则下列结论:①CF=AE;②OE=OF;③DE=BF;④图中共有四对全等三角形.其中正确结论的个数是( )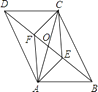
A.4
B.3
C.2
D.1
【答案】B
【解析】在ABCD中,CD//AB,CD=AB,
∴∠CDF=∠ABE,
∵AE⊥BD于点E,CF⊥BD于点F
∴∠CFD=∠AEB,
∴△CDF≌△ABE,
∴CF=AE,故①正确;
∵∠CFD=∠AEB,
∴CF//AE,
又∵CF=AE,
∴四边形AECF是平行四边形,
∴OE=OF,故②正确;
在ABCD中,OD=OB,
又∵OE=OF,
∴DE=BF,故③正确;
④图中共有6对全等三角形:△AOD≌△COB,△OCD≌△OAB,△CDF≌△ABE,△AFD≌△CEB,△OCF≌△OAE,△AOF≌△COE.故④错误.
综上,①②③正确.
故选B.
证明四边形AECF是平行四边形即可解答此题.

练习册系列答案
相关题目