Question

【题目】如图，EF∥AD，AD∥BC，CE平分∠BCF，∠DAC=120°，∠ACF=20°，求∠FEC的度数．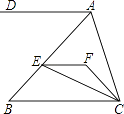

Answer 1

【答案】解：∵EF∥AD，AD∥BC，

∴EF∥BC，

∴∠ACB+∠DAC=180°，

∵∠DAC=120°，

∴∠ACB=60°，

又∵∠ACF=20°，

∴∠FCB=∠ACB﹣∠ACF=40°，

∵CE平分∠BCF，

∴∠BCE=20°，

∵EF∥BC，

∴∠FEC=∠ECB，

∴∠FEC=20°．

【解析】推出EF∥BC，根据平行线性质求出∠ACB，求出∠FCB，根据角平分线求出∠ECB，根据平行线的性质推出∠FEC=∠ECB，代入即可．
【考点精析】解答此题的关键在于理解平行线的判定与性质的相关知识，掌握由角的相等或互补（数量关系）的条件，得到两条直线平行（位置关系）这是平行线的判定；由平行线（位置关系）得到有关角相等或互补（数量关系）的结论是平行线的性质．