Question

【题目】已知一次函数y=kx+b的图象经过点A(1,1)和点B(1,3).求：

(1)求一次函数的表达式；

(2)求直线AB与坐标轴围成的三角形的面积；

(3)请在x轴上找到一点P，使得PA+PB最小，并求出P的坐标.

Answer 1

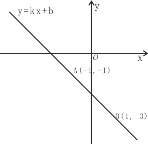
【答案】（1）y=-x-2；（2）2；（3）P（-）

【解析】（1）把A、B两点代入可求得k、b的值，可得到一次函数的表达式；

（2）分别令y=0、x=0可求得直线与两坐标轴的两交点坐标，可求得所围成的三角形的面积；

（3）根据轴对称的性质，找到点A关于x的对称点A′，连接BA′，则BA′与x轴的交点即为点P的位置，求出直线BA′的解析式，可得出点P的坐标．

（1）把A（-1，-1）B(1，-3)分别代入y=kx+b，得：

，解得：，

∴一次函数表达式为：y=-x-2；

（2）设直线与x轴交于C，与y轴交于D，y=0代入y=-x-2得x=-2，∴OC=2，

x=0代入y=-x-2 得：y=-2，∴OD=2，

∴S △COD =×OC×OD=×2×2=2；

（3）点A关于x的对称点A′，连接BA′交x轴于P，则P即为所求，

由对称知：A′(-1，1)，设直线A′B解析式为y=ax+c，

则有，解得：，

∴y=-2x-1，

令y=0得， -2x-1=0， 得x=- ，∴P（-）.