题目内容
【题目】借助一副三角板,可以得到一些平面图形
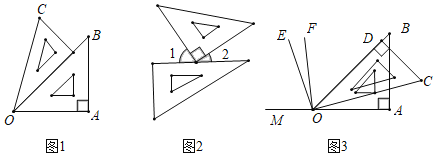
(1)如图1,∠AOC= 度.由射线OA,OB,OC组成的所有小于平角的和是多少度?
(2)如图2,∠1的度数比∠2度数的3倍还多30°,求∠2的度数;
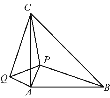
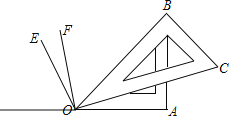
(3)利用图3,反向延长射线OA到M,OE平分∠BOM,OF平分∠COM,请按题意补全图(3),并求出∠EOF的度数.
【答案】(1)75°,150°;(2)15°;(3)15°.
【解析】
(1)根据三角板的特殊性角的度数,求出∠AOC即可,把∠AOC、∠BOC、∠AOB相加即可求出射线OA,OB,OC组成的所有小于平角的和;
(2)依题意设∠2=x,列等式,解方程求出即可;
(3)依据题意求出∠BOM,∠COM,再根据角平分线的性质得出∠MOE,∠MOF,即可求出∠EOF.
解:(1)∵∠BOC=30°,∠AOB=45°,
∴∠AOC=75°,
∴∠AOC+∠BOC+∠AOB=150°;
答:由射线OA,OB,OC组成的所有小于平角的和是150°;
故答案为:75;
(2)设∠2=x,则∠1=3x+30°,
∵∠1+∠2=90°,
∴x+3x+30°=90°,
∴x=15°,
∴∠2=15°,
答:∠2的度数是15°;
(3)如图所示,∵∠BOM=180°﹣45°=135°,∠COM=180°﹣15°=165°,
∵OE为∠BOM的平分线,OF为∠COM的平分线,
∴∠MOF=![]() ∠COM=82.5°,∠MOE=
∠COM=82.5°,∠MOE=![]() ∠MOB=67.5°,
∠MOB=67.5°,
∴∠EOF=∠MOF﹣∠MOE=15°.

练习册系列答案
相关题目