题目内容
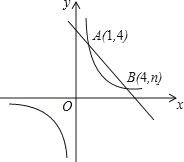
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
(1)求反比例函数和一次函数的解析式;
(2)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
【答案】(1)y=﹣x+5;(2)![]()
【解析】
(1)先把A点坐标代入y=![]() 中求出m得到反比例函数解析式为y=
中求出m得到反比例函数解析式为y=![]() ;再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
;再利用反比例函数解析式确定B点坐标,然后利用待定系数法求一次函数解析式;
(2)作B点关于x轴的对称点B′,连接AB′交x轴于P,如图,则B′(4,-1),利用两点之间线段最短可判断此时PA+PB的值最小,再利用待定系数法其凷直线AB′的解析式,然后求出它与x轴的交点坐标即可.
(1)把A(1,4)代入y=![]() 得m=1×4=4,
得m=1×4=4,
∴反比例函数解析式为y=![]() ;
;
把B(4,n)代入y=![]() 得4n=4,解得n=1,则B(4,1),
得4n=4,解得n=1,则B(4,1),
把A(1,4),B(4,1)代入y=kx+b得![]() ,解得
,解得![]() ,
,
∴一次函数解析式为y=﹣x+5;
(2)作B点关于x轴的对称点B′,连接AB′交x轴于P,如图,则B′(4,﹣1)
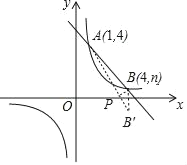
∵PA+PB=PA+PB′=AB′,
∴此时PA+PB的值最小,
易得直线AB′的解析式为y=![]() ,
,
当y=0时,![]() =0,解得x=
=0,解得x=![]() ,
,
∴P(![]() ,0).
,0).

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目