Question

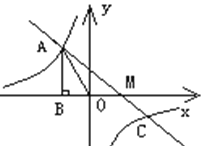
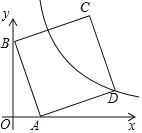
【题目】如图，在平面直角坐标系中，直线y＝﹣4x+4与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线y＝上；将正方形ABCD沿x轴负方向平移a个单位长度后，点C恰好落在双曲线在第一象限的分支上，则a的值是_____．

Answer 1

【答案】3

【解析】

根据直线的关系式可以求出A、B的坐标，由正方形可以通过作辅助线，构造全等三角形，进而求出C、D的坐标，求出反比例函数的关系式，进而求出C点 平移后落在反比例函数图象上的点G的坐标，进而得出平移的距离．

当x＝0时，y＝4，∴B（0，4），当y＝0时，x＝1，

∴A（1，0），

∴OA＝1，OB＝4，

∵ABCD是正方形，

∴AB＝BC＝CD＝DA，∠ABC＝∠BCD＝∠CDA＝∠DAB＝90°，

过点D、C作DM⊥x轴，CN⊥y轴，垂足为M、N，

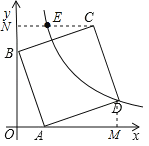
∴∠ABO＝∠BCN＝∠DAM，

∵∠AOB＝∠BNC＝∠AMD＝90°，

∴△AOB≌△BNC≌△DMA （AAS），

∴OA＝DM＝BN＝1，AM＝OB＝CN＝4

∴OM＝1+4＝5，ON＝4+1＝5，

∴C（4，5），D（5，1），

把D（5，1）代入y＝得：k＝5，

∴y＝，

当y＝5时，x＝1，

∴E（1，5），

点C向左平移到E时，平移距离为4﹣1＝3，即：a＝3，

故答案为：3．