题目内容
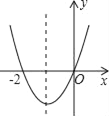
【题目】如图,根据二次函数y=ax2+bx+c(a≠0)的图象,有下列几种说法:
①a+b+c>0;
②该抛物线的对称轴是直线x=﹣1;
③当x=1时,y=2a;
④am2+bm+a>0(m≠﹣1).
其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】分析:①利用x=1时y>0进行分析判断;
②由抛物线经过(2,0),(0,0),可以判断出对称轴为直线![]()
③当x=1时,y=a+b+c,再结合抛物线的对称轴为![]() 可得
可得![]() ,抛物线经过原点得到c=0,据此进行推理分析;
,抛物线经过原点得到c=0,据此进行推理分析;
④由当x=m时,对应的函数值为![]() 当x=1时,对应的函数值为y=ab+c,
当x=1时,对应的函数值为y=ab+c,
并结合当![]() 时函数有最小值进行分析判断.
时函数有最小值进行分析判断.
详解:根据抛物线可知:当x=1时y>0,则有a+b+c>0,故①正确;
由二次函数的图象可知,抛物线经过点(2,0),(0,0),开口向上,
∴抛物线的对称轴为直线x=1,故②正确;
当x=1时,y=a+b+c,
∵抛物线的对称轴是直线x=1,
∴![]()
∴b=2a,
又∵抛物线经过(0,0),
∴c=0,
∴y=3a,故③错误;
当x=m时,对应的函数值为![]()
当x=1时,对应的函数值为y=ab+c,
又∵x=1时函数取得最小值,
∴![]() 即
即![]()
∵b=2a,
∴![]() (m≠1),故④正确;
(m≠1),故④正确;
故选C.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】列方程解应用题:某社区超市第一次用6000元购进甲、乙两种商品,其中甲商品的件数比乙商品件数的2倍少30件,甲、乙两种商品的进价和售价如表:
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲种商品的件数不变,乙种商品的件数是第一次的3倍;甲商品按原售价销售,乙商品在原售价上打折销售.第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多720元,求第二次乙种商品是按原价打几折销售?