题目内容
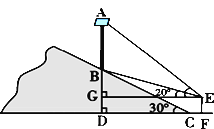
【题目】为了大力弘扬和践行社会主义核心价值观,某乡镇在一条公路旁的小山坡上,树立一块大型标语牌AB,如图所示,标语牌底部B点到山脚C点的距离BC为20米,山坡的坡角为30°. 某同学在山脚的平地F处测量该标语牌的高,测得点C到测角仪EF的水平距离CF = 1.7米,同时测得标语牌顶部A点的仰角为45°,底部B点的仰角为20°,求标语牌AB的高度.(参考数值:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,![]() )
)
【答案】标语牌AB的高度约为12.16米.
【解析】分析:![]() 解直角三角形求处CD的长度,则
解直角三角形求处CD的长度,则![]() 然后在直角
然后在直角![]() 中即可求得
中即可求得![]() 的长,在Rt△AGE中,求得
的长,在Rt△AGE中,求得![]() 的长,从而求得
的长,从而求得![]() 的高度..
的高度..
详解:在Rt△BDC中,![]() BC = 20米,
BC = 20米,![]()
∴![]()
∴![]()
∴![]()
在Rt△BGE中,![]()
∴![]()
在Rt△AGE中,![]()
∴![]()
∴![]()
答:标语牌AB的高度约为12.16米.
点睛:考查解直角三角形的应用,结合图形利用三角函数解三角形即可.
【题型】解答题
【结束】
20
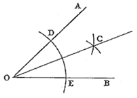
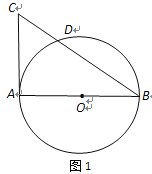
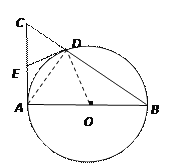
【题目】已知AB是⊙O的直径,AC是⊙O的切线,BC交⊙O于点D(如图1).
(1)若AB=2,∠B=30°,求CD的长;
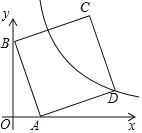
(2) 取AC的中点E,连结D、E(如图2),求证:DE与⊙O相切.
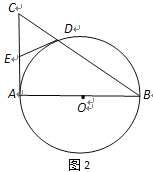
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】分析:![]() 连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得
连接AD ,根据AC是⊙O的切线,AB是⊙O的直径,得到∠CAB=∠ADB=90°,根据∠B=30°,解直角三角形求得![]() 的长度.
的长度.
![]() 连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
连接OD,AD.根据DE=CE=EA,∠EDA=∠EAD. 根据OD=OA,得到
∠ODA=∠DAO,得到∠EDA+∠ODA=∠EAD+∠DAO.得到∠EDO=90°即可.
详解:(1)如图,连接AD ,
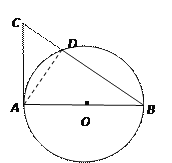
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=90°,
∴ΔCAB,ΔCAD均是直角三角形.
∴∠CAD=∠B=30°.
在RtΔCAB中,AC=ABtan30°=![]()
∴在RtΔCAD中,CD=ACsin30°=![]()
(2)如图,连接OD,AD.
∵AC是⊙O的切线,AB是⊙O的直径,
∴∠CAB=∠ADB=∠ADC=90°,
又∵E为AC中点,
∴DE=CE=EA,
∴∠EDA=∠EAD.
∵OD=OA,
∴∠ODA=∠DAO,
∴∠EDA+∠ODA=∠EAD+∠DAO.
即:∠EDO=∠EAO=90°.
又点D在⊙O上,因此DE与⊙O相切.

 习题精选系列答案
习题精选系列答案