题目内容
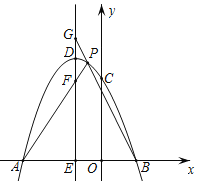
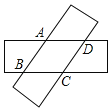
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 交x轴于点A、点
交x轴于点A、点![]() 点A在点B的左边
点A在点B的左边![]() ,交y轴于点C,直线
,交y轴于点C,直线![]() 经过点B,交y轴于点D,且
经过点B,交y轴于点D,且![]() ,
,![]() .
.
![]() 求b、c的值;
求b、c的值;
![]() 点
点![]() 在第一象限,连接OP、BP,若
在第一象限,连接OP、BP,若![]() ,求点P的坐标,并直接判断点P是否在该抛物线上;
,求点P的坐标,并直接判断点P是否在该抛物线上;
![]() 在
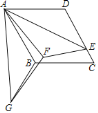
在![]() 的条件下,连接PD,过点P作
的条件下,连接PD,过点P作![]() ,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作
,交抛物线于点F,点E为线段PF上一点,连接DE和BE,BE交PD于点G,过点E作![]() ,垂足为H,若
,垂足为H,若![]() ,求
,求![]() 的值.
的值.
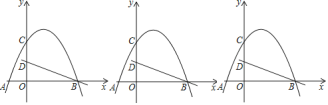
【答案】(1)![]() ;(2)
;(2)![]() ,点P在抛物线上;(3)2.
,点P在抛物线上;(3)2.
【解析】
(1)直线y=kx-6k,令y=0,则B(6,0),便可求出点D、C的坐标,将B、C代入抛物线中,即可求得b、c的值;
(2)过点P,作![]() 轴于点L,过点B作
轴于点L,过点B作![]() 于点T,先求出点P的坐标为(4,4),再代入抛物线进行判断即可;
于点T,先求出点P的坐标为(4,4),再代入抛物线进行判断即可;
(3)连接PC,过点D作DM⊥BE于点M,先证△PCD≌△PLB,再分别证四边形EHKP、FDKP为矩形,求得![]() =2.
=2.
解:![]() 如图,直线
如图,直线![]() 经过点B,
经过点B,
令![]() ,则
,则![]() ,即
,即![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,点
,点![]() ,
,
![]() 点B、C在抛物线
点B、C在抛物线![]() 上,
上,
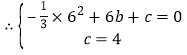 ,解得:
,解得:![]() ,
,
函数表达式为:![]() ;
;
![]() 如图,过点P,作
如图,过点P,作![]() 轴于点L,过点B作
轴于点L,过点B作![]() 于点T,
于点T,
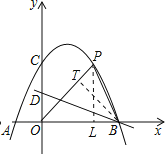
![]() ,
,
![]() ,
,![]() ,
,
![]() 点
点![]() 在第一象限,
在第一象限,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,
,
故点P在抛物线上;
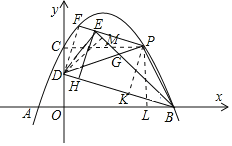
![]() 如图,连接PC,
如图,连接PC,
![]() ,
,![]() ,
,
![]() 轴,
轴,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
过点P作![]() 于点K,连接DF,
于点K,连接DF,
![]() ,
,![]() ,
,
![]() ,
,![]() 四边形EHKP为平行四边形,
四边形EHKP为平行四边形,
![]() ,
,![]() 四边形EHKP为矩形,
四边形EHKP为矩形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
过点D作![]() 于点M,
于点M,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() 直线PF与BD解析式中的k值相等,
直线PF与BD解析式中的k值相等,
![]() ,
,
联立![]() 并解得:
并解得:![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() 四边形FDKP为平行四边形,
四边形FDKP为平行四边形,
![]() ,
,![]() 四边形FDKP为矩形,
四边形FDKP为矩形,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目