题目内容
如图，等边三角形ABC中，点D、E、F分别是BC、AC、AB上的点，且DE⊥AC，EF⊥AB，FD⊥BC，垂足分别为点E、F、D. 则△DEF的面积与△ABC的面积之比等于 （ ）
A.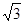
︰2 B. 1︰3 C. 2︰3 D. 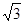︰3
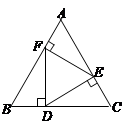
A.
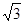︰2 B. 1︰3 C. 2︰3 D. 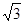︰3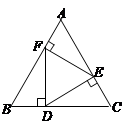B
：∵DE⊥AC，EF⊥AB，FD⊥BC，
∴∠C+∠EDC=90°，∠FDE+∠EDC=90°，
∴∠C=∠FDE，
同理可得：∠B=∠DFE，∠A=DEF，
∴△DEF∽△CAB，
∴△DEF与△ABC的面积之比=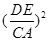
，
又∵△ABC为正三角形，
∴∠B=∠C=∠A=60°，△EFD是等边三角形，
∴EF=DE=DF，
又∵DE⊥AC，EF⊥AB，FD⊥BC，
∴△AEF≌△CDE≌△BFD，
∴BF=AE=CD，AF=BD=DC，
在Rt△DEC中，
DE=DC×sin∠C=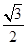
DC，EC=cos∠C×DC= 
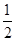DC，
又∵DC+BD="BC=A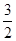C="
DC，
∴
，
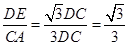∴△DEF与△ABC的面积之比等于：=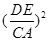
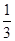=1：3．
故选B．
∴∠C+∠EDC=90°，∠FDE+∠EDC=90°，
∴∠C=∠FDE，
同理可得：∠B=∠DFE，∠A=DEF，
∴△DEF∽△CAB，
∴△DEF与△ABC的面积之比=
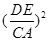，又∵△ABC为正三角形，
∴∠B=∠C=∠A=60°，△EFD是等边三角形，
∴EF=DE=DF，
又∵DE⊥AC，EF⊥AB，FD⊥BC，
∴△AEF≌△CDE≌△BFD，
∴BF=AE=CD，AF=BD=DC，
在Rt△DEC中，
DE=DC×sin∠C=
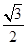DC，EC=cos∠C×DC= 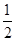DC，又∵DC+BD="BC=AC="
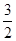DC，∴
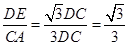，∴△DEF与△ABC的面积之比等于：
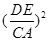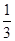==1：3．故选B．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目
，若sinA＝
,那么tanB等于（ ）
中，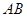
、
、
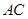三边的长分别为
、
、
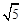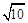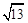，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点
、
、
（
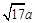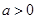），请利用图②的正方形网格（每个小正方形的边长为
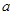）画出相应的
、
、
（
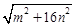，且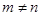
），试运用构图法求出这三角形的面积．
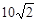海里．求：
，AB=8cm，AC=4cm，则△ABC的面积= cm2．
交AC于点E，F是
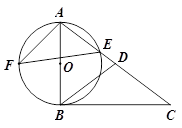
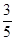，AE=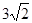
，求sinF的值和AF的长．